2. Laser

The Boltzmann distribution

A prior condition for producing laser light is is the induced emission of photons. This must occur more frequently than absorption and spontaneous emission. These balances are investigated more thoroughly in supplement 1. Another look at the graph on the previous page ...

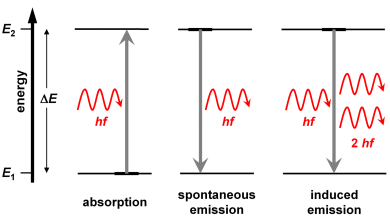
... shows that there must be more atoms in the higher energy state E₂ than in the lower state E₁: then photons having a suitable energy ΔE will provoke an induced emission instead of absorption. It is denoted as population inversion if the state E₂ is occupied by more atoms than the state E₁.

The term population inversion indicates that deeper energy levels are normally occupied by more atoms than the higher states. Denoting the number of atoms in state E₁ as N₁, and the number of atoms in state E₂ as N₂, then it is normally N₁>N₂. In case of a population inversion it should be: N₁<N₂.

Can we calculate N₁ and N₂? Possibly yes, if the system (the atoms or molecules) does not transmit or receive energy from outside. After a while, the values of N₁ and N₂ do not change any more and reach an equilibrium. This is called the thermodynamic equilibrium. The ratio of N₁ and N₂ is then given by the Boltzmann distribution

where T is the absolute (Kelvin) temperature. Obviously, the population ratio depends only on temperature! The factor k is the Boltzmann constant, it is k=1.38·10^-23 J K.

The graph below shows a Boltzmann distribution. It has been calculated with energy levels that are used to produce the laser light of a HeNe laser having the wavelength 633 nm. Here it is: E₂-E₁=3.1·10^-19 J.

Boltzmann distribution of the HeNe laser energy levels which produce the 633 nm laser light.

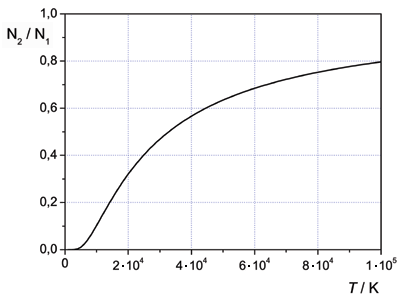
We observe that even with a temperature of 100 000 K, the level E₁ has a higher population than E₂. At room temperature, the population ratio is so small that it is quite indistinguishable from the zero line.