Supplement 4.3: Polarisatie van elektromagnetische golven: Een inleiding

De eerste benadering

Op pagina 2 van het gedeelte over elektromagnetische golven hebben we vergelijkingen ontwikkeld voor het elektrische en magnetische veld van een monochromatische vlakke golf:

E (x, t) = E_{o} sin 2 π (\frac{x}{λ} - \frac{t}{T}) B (x, t) = B_{o} sin 2 π (\frac{x}{λ} - \frac{t}{T})

Door het periodieke gedrag van de sinusfunctie in $2 π$ vertonen de vergelijkingen de periodiciteit met de golflengte λ en de periode T. In plaats van deze grootheden zijn andere parameters die de factor $2 π$ bevatten nuttig omdat de vergelijkingen dan veel korter geschreven kunnen worden. Deze zijn:

het golfgetal $k = \frac{2 π}{λ}$
de hoekfrequentie $ω = \frac{2 π}{T} = 2 π f$

Wat betekent dat:

E (x, t) = E_{o} sin (k x - ω t) B (x, t) = B_{o} sin (k x - ω t)

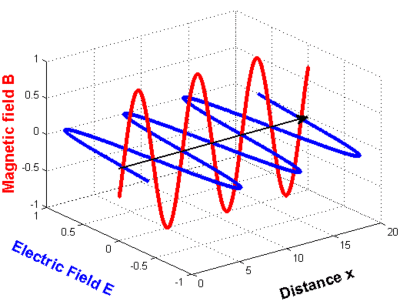
Zo ziet de golf eruit in een grafiek:

Een elektromagnetische golf die zich van links naar rechts langs de x as voortplant. De krommen tonen de piekposities van beide veldvectoren, die loodrecht op de x-as staan (zwarte pijl). Animatie.

De oscillaties van het elektrische en magnetische veld zijn duidelijk zeer regelmatig voor deze golf. Dit wordt een gepolariseerde golf genoemd. Een golf wordt ongepolariseerd genoemd als de oscillaties volledig onregelmatig zijn. Golven kunnen gedeeltelijk gepolariseerd zijn.
Alleen transversale golven - bijvoorbeeld elektromagnetische golven - kunnen gepolariseerd zijn. Longitudinale golven - bijvoorbeeld geluidsgolven - zijn niet gepolariseerd.

In de bovenstaande grafiek wordt niets gezegd over de richting van het elektrische en magnetische veld (behalve dat ze loodrecht op elkaar en op de voortplantingsrichting staan): y- en z-coördinaten ontbreken om de richting van de veldsterktedectoren weer te geven.

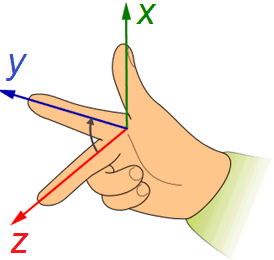
We onderzoeken nu een golf die zich voortplant in x-richting in een driedimensionaal rechtshandig $(x, y, z)$ coördinatenstelsel. Alleen het elektrisch veld wordt bekeken; de resultaten gelden ook voor het orthogonaal oscillerend magnetisch veld.

Links- en rechtshandige cartesiaanse coördinaten.

De veldvector $\vec{E}$ staat loodrecht op de voortplantingsrichting x. Hij wordt gesplitst in componenten langs richtingen y en z:

E_{y} = E_{y, o} sin (k x - ω t) E_{z} = E_{z, o} sin (k x - ω t + φ)

$E_{y, o}$ en $E_{z, o}$ zijn de amplituden. De grootheid $φ$ geeft de faseverschuiving tussen de twee componenten aan. Voor een monochromatische golf is $φ$ constant, beide golfcomponenten zijn dus coherent.

De waarden van

E_{y, o}

E_{z, o}

φ

karakteriseren volledig het type polarisatie van een monochromatische golf: Deze kan lineair, cirkelvormig of elliptisch zijn.

De belangrijkste soorten polarisatie en hun oscillatiekarakteristieken, $n$ is een geheel getal:

Conditie	Type polarisatie
$E_{z, o} = 0$	linear langs de y-as
$E_{y, o} = 0$	linear langs de z-as
$φ = 2 n π, E_{y} = \frac{E_{y, o}}{E_{z, o}} E_{z}$	linear diagonaal in het eerste en derde kwadrant van het y,z-vlak
$φ = (2 n + 1) π, E_{y} = - \frac{E_{y, o}}{E_{z, o}} E_{z}$	linear diagonaal in het tweede en vierde kwadrant van het y,z-vlak
$φ = (2 n - \frac{1}{2}) π, E_{y, o} = E_{z, o}$	rechts cirkelvormig: De veldvectoren draaien naar rechts (in de richting van de golf). *Animatie* van de draaiende vectorkoppen, het E-veld wordt in blauw weergegeven, het B-veld in rood.
$φ = (2 n + \frac{1}{2}) π, E_{y, o} = E_{z, o}$	links cirkelvormig: De veldvector draait naar links (in de richting van de golf)
$φ = (2 n - \frac{1}{2}) π, E_{y, o} \neq E_{z, o}$	rechts elliptisch: De veldvectoren draaien naar rechts (in de richting van de golf). *Animatie* van de draaiende vectorkoppen, het E-veld wordt blauw weergegeven, het B-veld rood.
$φ = φ (t), E_{y, o} = E_{z, o}$	ongepolariseerd, natuurlijk licht

Natuurlijk licht is niet monochromatisch maar heeft een breed spectraal bereik, $φ$ verandert statistisch permanent. Dee y en z-componenten zijn niet coherent met elkaar.

Gedeeltelijk gepolariseerd licht bestaat uit gepolariseerd en ongepolariseerd licht. Het wordt gekarakteriseerd door de mate van polarisatie:

p = (Intensiteit van het gepolariseerde deel)/Totale intensiteit

Voor de karakterisering van gedeeltelijk gepolariseerd licht zijn vier grootheden nodig: De waarden van