4. Absorptie en verstrooiing

Wat wiskunde

We beginnen met een focus op de kleinste - oneindig kleine - schaal binnen een absorberende stof die vanaf de linkerkant wordt verlicht. Het licht heeft een intensiteit van $I$ in het punt $x$ . Slechts een oneindig kleine stap $d x$ verder, in het punt $x + d x$ , is de intensiteit met een oneindig kleine hoeveelheid $d I$ , afgenomen, zodat het kan worden beschreven als $I - d I$ .

Licht plant zich voort van links naar rechts in een absorberend medium. In het punt x is de intensiteit gelijk aan I, terwijl deze in het punt x+dx is afgenomen tot I-dI.

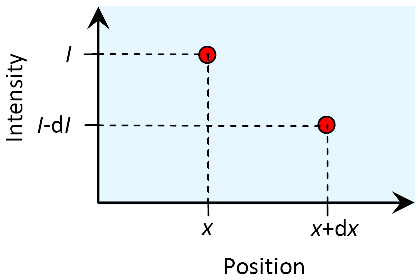
Er wordt aangenomen dat de afname $- d I$ evenredig is met $I$ en $d x$ :

- d I ~ I d x

Bovendien is de afname afhankelijk van de absorptie-eigenschappen van de stof. Deze speciale eigenschappen worden gekarakteriseerd door de absorptiecoëfficiënt a, waardoor proportionaliteit een vergelijking wordt:

- d I = a I d x

Door transformatie wordt de volgende differentiaalvergelijking verkregen:

\frac{d I}{d x} = - a I

die nu moet worden opgelost (of: geïntegreerd). In woorden is de oplossing gemakkelijk te vinden:

"Gevraagd is de intensiteit $I$ , ..."
links: "...waarvan de differentiatie ten opzichte van $x$ ..."
rechts: "... resulteert in $I$ met de extra factor $- a$ ."

De functie die dat kan is de exponentiële functie: Hij blijft bestaan wanneer hij wordt afgeleid of geïntegreerd. Een mogelijke aanpak voor het oplossen van het probleem is dus:

I = e^{- a x}

wat leidt tot de initiële differentiaalvergelijking wanneer deze wordt gedifferentieerd ten opzichte van $x$ :

\frac{d I}{d x} = - a e^{- a x} = - a I

Daarom is de exponentiële vergelijking de weg naar de oplossing.

In het punt $x = 0$ moet de intensiteit gelijk zijn aan $I_{o}$ (Laat dit de intensiteit aan het begin zijn, de vorige benadering geeft $x = 0$ voor de waarde 1), en moet worden ingevuld aan de rechterkant van de vergelijking. Dit leidt tot de uiteindelijke oplossing:

I (x) = I_{o} e^{- a x}

Exponentieel of lineair? ↓

In de linkerkolom hebben we aangenomen dat de infinitesimale afname $- d I$ evenredig zou zijn met de infinitesimale afstanden $d x$ . Evenredig gedrag wijst erop dat de intensiteit evenredig zou afnemen op de weg $x$ . We hebben onlangs ontdekt dat de intensiteit exponentieel afneemt. Hoe past dat?

Antwoord: (Maar beslis eerst zelf!)
Voor een oneindig klein interval $d x$ kan de exponentiële functie benaderd worden door een raaklijn waarvan de helling $d I / d x = - a e^{- a x}$ is met de betreffende waarde van $x$ . Dit komt overeen met de lineaire benadering voor oneindig kleine afstanden. Voor langere afstanden, wat de integratie van de differentiaalvergelijking betekent, zal het resultaat de exponentiële kromme zijn.

Vergelijkingen ↓

Wet van Lambert: De intensiteit van licht neemt exponentieel af in functie van de afstand x. Dat wordt in de volgende afbeeldingen getoond aan de hand van het voorbeeld van de absorptie van laserlicht door groene pigmenten in planten.

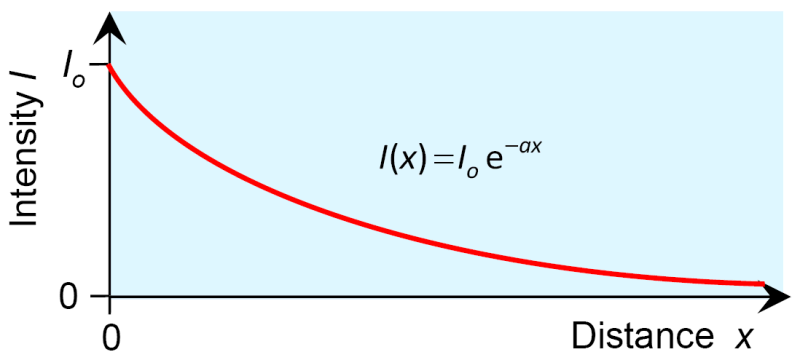
Dit is de wet van Lambert: De intensiteit van licht neemt exponentieel af op zijn weg door een absorberend medium, terwijl de afname afhangt van de absorptiecoëfficiënt $a$ van het medium.

405 nm 532 nm 650 nm Chlorofyl absorptie

Chlorofyl a werd met alcohol uit de bladeren van de plant geëxtraheerd. De groenachtige oplossing (in een glazen cuvet) wordt verlicht door laserstralen van links. Chlorofyl absorbeert blauw licht. Bijgevolg neemt de helderheid van de blauwe straal (golflengte 405 nm) af van links naar rechts. De rode gloed wordt veroorzaakt door de rode fluorescentie die chlorofyl uitzendt wanneer het blauw licht absorbeert. De groene laserstraal (532 nm) vertoont geen waarneembare afname van helderheid, de rode laserstraal (650 nm) slechts een kleine. Omdat de absorptie van chlorofyl op verschillende golflengten van invloed is, nemen de laserstralen op verschillende punten van de cuvet anders af.
Bron van het absorptiespectrum van chlorofyl a: PhotochemCAD. Het spectrum toont de molaire decadische absorptiecoëfficiënt, die zal worden uitgelegd in Supplement 4.1.

De afmeting van de absorptiecoëfficiënt is een inverse lengte. Afhankelijk van de waarde kan deze in verschillende eenheden worden weergegeven:

voor de wolkenvrije atmosfeer meestal in 1/km,
voor water in 1/m,
voor sterk absorberende materialen (bijv. vlekken van milieuvervuiling door ruwe olie) in 1/μm.

Inzicht in Spectra van de Aarde

4. Absorptie en verstrooiing

Wat wiskunde