4. Absorption et diffusion

Quelques mathématiques

Nous commençons par nous concentrer sur l'échelle la plus petite - infinitésimale - à l'intérieur d'une substance absorbante qui est éclairée du côté gauche. La lumière a une intensité de $I$ au point $x$. Seulement un pas infinitésimal $\text{d}x$ plus loin, au point $x+\text{d}x$, l'intensité a diminué d'une quantité infinitésimale $\text{d}I$, de sorte qu'elle peut être décrite comme $I-\text{d}I$.

La lumière se propage de la gauche vers la droite dans un milieu absorbant. Au point x, l'intensité est égale à I, tandis qu'elle diminue à I-dI au point x+dx.

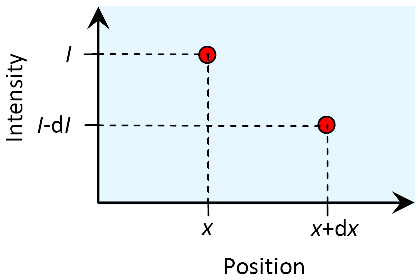
La décroissance $-\text{d}I$ est supposée proportionnelle à $I$ et $\text{d}x$:

En outre, la diminution dépend des caractéristiques d'absorption de la substance. Ces propriétés particulières seront caractérisées par le coefficient d'absorption a, ce qui fait de la proportionnalité une équation :

Par transformation, on obtient l'équation différentielle suivante :

qui doit maintenant être résolue (ou : intégrée). Lorsqu'elle est formulée avec des mots, la solution est facile à trouver :

  "Interrogée est l'intensité $I$, ..."
  à gauche : "...dont la différenciation par rapport à $x$..."
  à droite : "... aboutit à $I$ avec le facteur supplémentaire $-a$ ."

La fonction capable de faire cela est la fonction exponentielle : Elle persiste lorsqu'elle est dérivée ou intégrée. Une approche possible pour résoudre le problème est donc la suivante :

ce qui conduit à l'équation différentielle initiale lorsqu'on la différencie par rapport à $x$:

Par conséquent, l'équation exponentielle permet de trouver la solution.

Au point $x=0$, l'intensité est égale à $I_o$ ((il s'agit de l'intensité au début, l'approche précédente donne $x=0$ pour la valeur 1), et doit être complétée sur le côté droit de l'équation. Cela conduit à la solution finale :

Loi de Lambert : L'intensité de la lumière diminue exponentiellement en fonction de la distance x. Cela est illustré dans les images suivantes par l'exemple de l'absorption de la lumière laser par les pigments verts des plantes.

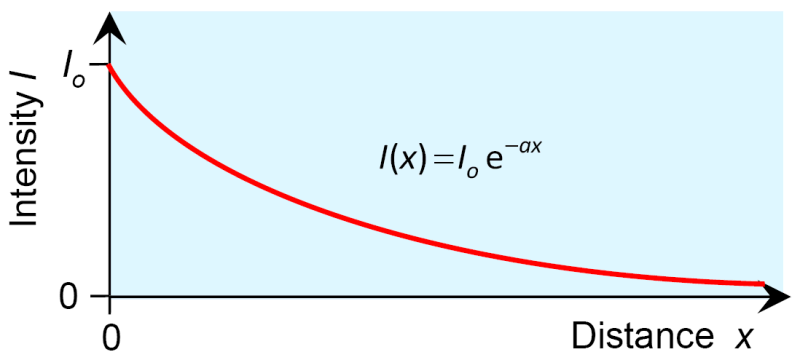
C'est la loi de Lambert : L'intensité de la lumière décroît exponentiellement à travers un milieu absorbant, la décroissance dépendant du coefficient d'absorption $a$.

405 nm 532 nm 650 nm Absorption de la chlorophylle

La chlorophylle a a été extraite des feuilles de plantes à l'aide d'alcool. La solution verdâtre (dans une cuvette en verre) est éclairée par des faisceaux laser provenant de la gauche. La chlorophylle absorbe la lumière bleue. Par conséquent, la luminosité du faisceau bleu (longueur d'onde de 405 nm) diminue de gauche à droite. La lueur rouge est créée par la fluorescence rouge que la chlorophylle émet lorsqu'elle absorbe la lumière bleue. Le faisceau laser vert (532 nm) ne présente pas de baisse de luminosité perceptible, tandis que le faisceau laser rouge (650 nm) n'en présente qu'une faible. Comme ils sont influencés par l'absorption de la chlorophylle à différentes longueurs d'onde, les faisceaux laser diminuent différemment en différents points de la cuvette.
Source du spectre d'absorption de la chlorophylle a : PhotochemCAD. Le spectre montre le coefficient d'absorption molaire décadique, qui sera expliqué dans le supplément 4.1.

La dimension du coefficient d'absorption est une longueur inverse. Selon sa valeur, il peut être donné en différentes unités :

• pour l'atmosphère sans nuages, la plupart du temps en 1/km,
• pour les eaux, en 1/m,
• pour les matériaux fortement absorbants (par exemple, les points de pollution environnementale par le pétrole brut) en 1/μm.