3. Climate and climate change

The greenhouse effect    (1/4)

In the years 1951 to 1980 the mean temperature over the land and the oceans on the Earth's surface was about 14°C. It remained quite stable during this time. This period is therefore referred to as a climatological reference period in climate research. Since then, until today a temperature increase of about 1°C is observed, which does affect the climate.

We often hear or read about the greenhouse effect as the cause of threatening climate change. That's only part of the truth. We can estimate, with the information presented so far, what temperatures the Earth would have without the greenhouse effect; i.e. when there are no greenhouse gases in the atmosphere.

Solar radiation

First, we need to calculate the radiation generated by the sun. The radiation temperature of its photosphere is Trad,S = 5772 K. According to the Stefan-Boltzmann law, the specific radiation on the solar surface is equal to

M=σ T rad,S 4 =5.67⋅ 10 −8 W m 2    K 4 ⋅ 5772 4    K 4 =62.9⋅ 10 6 W m 2 .

This means: every square metre of the sun has an output of approx. 63 MW! With the radius of the sun RS = 700 000 km = 700·106 m the result for the entire solar surface is the radiative power:

4π R S 2 M=387.5⋅ 10 24 W

It's good that the Earth doesn't get too close to the sun! How strong is the radiation at Earth's distance from the sun?

The mean distance of the Earth to the sun is 149 589 000 km, which is commonly denoted 1 AU; AU stands for astronomical unit. Let's create an imaginary sphere with this radius with the sun at the centre and calculate the radiation per square metre on the spherical surface; so we get the radiation per square metre that arrives on the Earth. To do this we divide the total radiation of the sun through the spherical surface area:

Total radiative power Spherical surface = 387.5⋅ 10 24 W 4π⋅ (149.6⋅ 10 9 ) 2    m 2 =1378   W m 2
Equations ↓
Zoom Sign
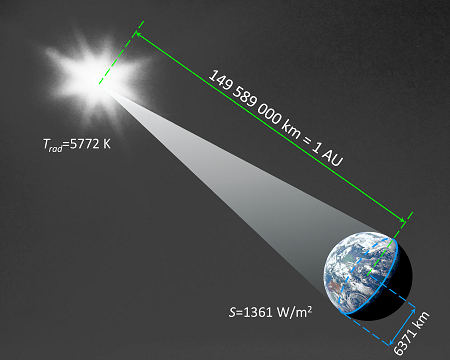
Sun and Earth

The sun and the Earth at a distance of 1 AU, the astronomical unit. The sun radiates with the temperature Trad. The Earth's radius RE and the solar constant S are also indicated.
Source: Rainer Reuter, University of Oldenburg, Germany.

The calculated 1378 W/m² is close to the previously estimated 1500 W/m². The deviation from the solar constant S = 1361  W/m² is only about 1.2%. In the following calculations we will use this value of the solar constant.