Supplement 2.2: De stralingswet van Planck (1/2)
Max Planck veronderstelde het concept van een holte: De straling ervan is in thermisch evenwicht met het oppervlak van de interne ruimte. De atomen van het oppervlak absorberen alle inkomende straling. Ondertussen zenden ze elektromagnetische golven uit die gehoorzamen aan de stralingswet van Kirchhoff met de hoogste emissiegraad die mogelijk is voor zwarte lichamen.
Een tweede conceptuele reflectie betreft de energie van de golven die worden uitgezonden door de atomen van het oppervlak. Deze golven zijn verbonden met de oscillerende atomen, de zogenaamde oscillatoren. Volgens de klassieke natuurkunde worden dergelijke energiewaarden continu verdeeld: De trillingsenergie in een klassiek oscillerend systeem kan continu verdeelde waarden aannemen. Planck veronderstelde echter dat deze energieën gekwantiseerd zijn. Daarom konden ze alleen discrete waarden aannemen. Dit was in tegenspraak met de klassieke fysica, maar leidde tot de juiste conclusie en vormt daarom de basis van een nieuwe ontwikkeling, de kwantumtheorie.
Golven in een holte
We observeren een klein bereik van het spectrum bij een frequentie en de huidige energiedichtheid van de golven in een oneindig klein frequentieinterval . Het is schijnbaar uit te drukken door de midspectrale energiedichtheid van een enkele golf, vermenigvuldigd met de bestaande golven in het interval .
Het aantal van deze golven kan worden geschat. In overeenstemming met de Maxwell-theorie van elektromagnetische golven is de elektrische veldsterkte nul aan het oppervlak. Hier kunnen alleen stationaire golven met knooppunten van oscillatie verschijnen, als hun golflengte in een holte van de binnenste omvang kwalificeert als:
verder geldt: Alleen gehele veelvouden van de gehalveerde golflengte passen in de afstand , als men veronderstelt dat er een knooppunt aan de randen verschijnt. De mogelijke golflengtes zijn dus niet continu maar discreet verdeeld; ze vormen de intrinsieke osillaties, bekend als modi, van de holte.
De golfgetallen resp. frequenties komen dus overeen met:
Door de laatste relatie te herformuleren en te differentiëren, volgt voor het vereiste aantal oscillatiemodes in het frequentieinterval:
Nu moet er rekening worden gehouden met de driedimensionaliteit van de holte, zoals de eigenschappen van de golven om te oscilleren in drie dimensies x, y en z. Dienovereenkomstig zijn er discrete getalwaarden nx, ny and nz voor deze coördinaatrichtingen. Hoeveel golven zijn er in totaal aanwezig in de leegte?
Om dat te vinden, onderzoeken we de golven in een driedimensionale ruimte met de coördinaten nx, ny and nz. De overeenkomstige golven voor het frequentieinterval liggen in een spericale schil van die ruimte met de straal
en de dikte . Het volume is het resultaat van de vermenigvuldiging van het oppervlak van de bol met de dikte van de schelp .
Uitsluitend positieve waarden voor nx, ny en nz zijn legitiem (de golflengtes in de voorwaarden voor stationaire golven zijn positief). Slechts in één van de acht octanten van het coórdinatenstelsel zijn alle waarden positief. Dit is dus de enige die is toegestaan.
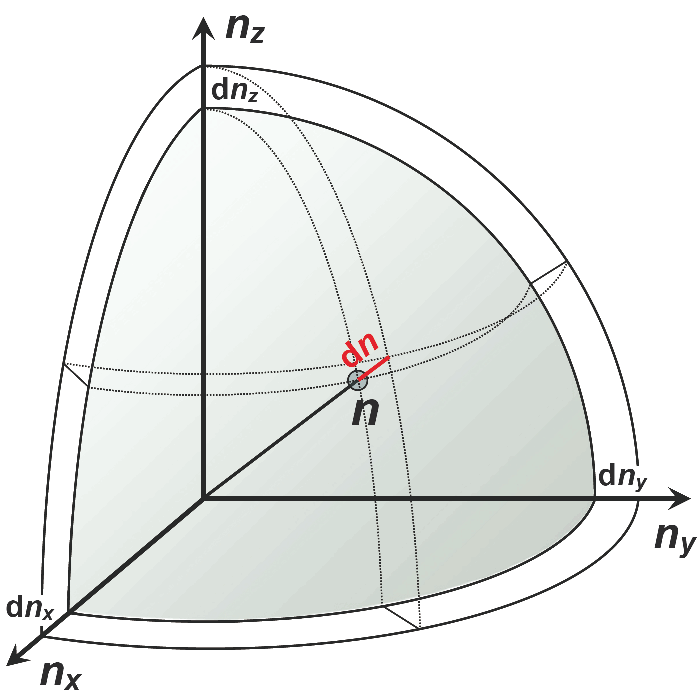
Driedimensionale ruimte van mogelijke oscillatormodi van stationaire golven in een holte. Alleen de octant met uitsluitend positieve waarden is afgebeeld.
Elke golf kan verschijnen met twee orthogonale polarisaties waarmee rekening moet worden gehouden door de factor 2. Dit levert het aantal oscillatietoestanden op door de rekenkundige uitdrukkingen voor en toe te passen:
Hierbij wordt, zonder beperking van de algemeenheid, verondersteld dat de holte dezelfde uitzetting heeft in alle drie de dimensies. Met het volume wordt het aantal toestanden van de holte in het frequentieinterval verkregen:
