2. Thermal Radiation

Absorption and emission: Kirchhoff's radiation law     (1/4)

Absorption and emission

Gustav Kirchhoff examined the interplay between absorption of electromagetic waves by matter and the emission of thermal radiation. Absorption is characterised through the transformation of incoming radiation into other forms of energy, particularly heat, but chemical energy as well, such as in photosynthesis of plants.

Besides that, matter can reflect or transmit radiation (what means that it is permeable for radiation). A glass panel is free of absorption in the visible light, whereas it reflects about 10% of the incoming light intensity. That might be different for other spectral ranges: Infrared radiation beyond 3.5 μm is absorbed by glass, a glass panel is thus opaque. A black cloth absorbs the visible light, in the near infrared from 1 μm on, it reflects the radiation though. Obviously those characteristics are dependent on the examined spectral ranges.

Absorption can be characterised by the degree of absorption $\alpha$. It indicates what part of the incoming radiation to a body is absorbed by it:

• $\alpha =1$ indicates total absorption what is a characteristic of black bodies
• $\alpha =0$ equals total transmission or reflection of radiation. Such objects are called white bodies
• equals $\alpha$ any value between 0 and 1, you are dealing with a grey body.

The ability to emit radiation, the degree of emission $\epsilon$ for thermal radiation can be represented in an equal manner.

• $\epsilon =0$ indicates the absence of emission
• $\epsilon =1$ represents the maximum of emission possible.

Balance of absorption and emission

We look at two bodies in a box. One of them is black, the other is white (picture in right column). The cavity shall be totally isolated from the environment. Therefore the bodies would not take up any energy as heat or radiation from the environment. Non of them emits energy to the environment either.

Both bodies emit thermal radiation (the interior walls of the box are of importance but in this section we will not focus on them). The black body absorbs more radiation than the white one. Because of this imbalance, at a first glance the temperature of the black body should increase whereas the temperature of the white body should decrease: This could be one of the most important inventions for the function of the fridge and a heater!

In reality one observes that the temperature of such bodies approximate to each other and will be equal after some time: The system then is in a thermal equilibrium. This assertion, built on experience, is called the zeroth law of thermodynamics.

This obvious contradiction between expectation and experience may be explained be the following assumption: The degrees of absorption and emission would behave similarly. The black body in comparison to the white absorbs more radiation due to its high degree of absorption. At the same time it would emit more radiation as well.

If the two bodies have different temperatures in the beginning, they would approximate over time. This is due to the temperature depending emission of radiation, while the absorption is not (or at least very few) temperature dependent. The bodies finally reach an isothermal state. To make this come true, is has to be:

or:                                             $\alpha /\epsilon =1$.

Two bodies in a thermal equilibrium within a cavity isolated from the environment. The arrows depict the radiant powers. The letters e and a stand for the emitted and absorbed radiation of the white body. There is an exchange of radiation between the bodies and the inner walls of the cavity but this is not considered in the graph.

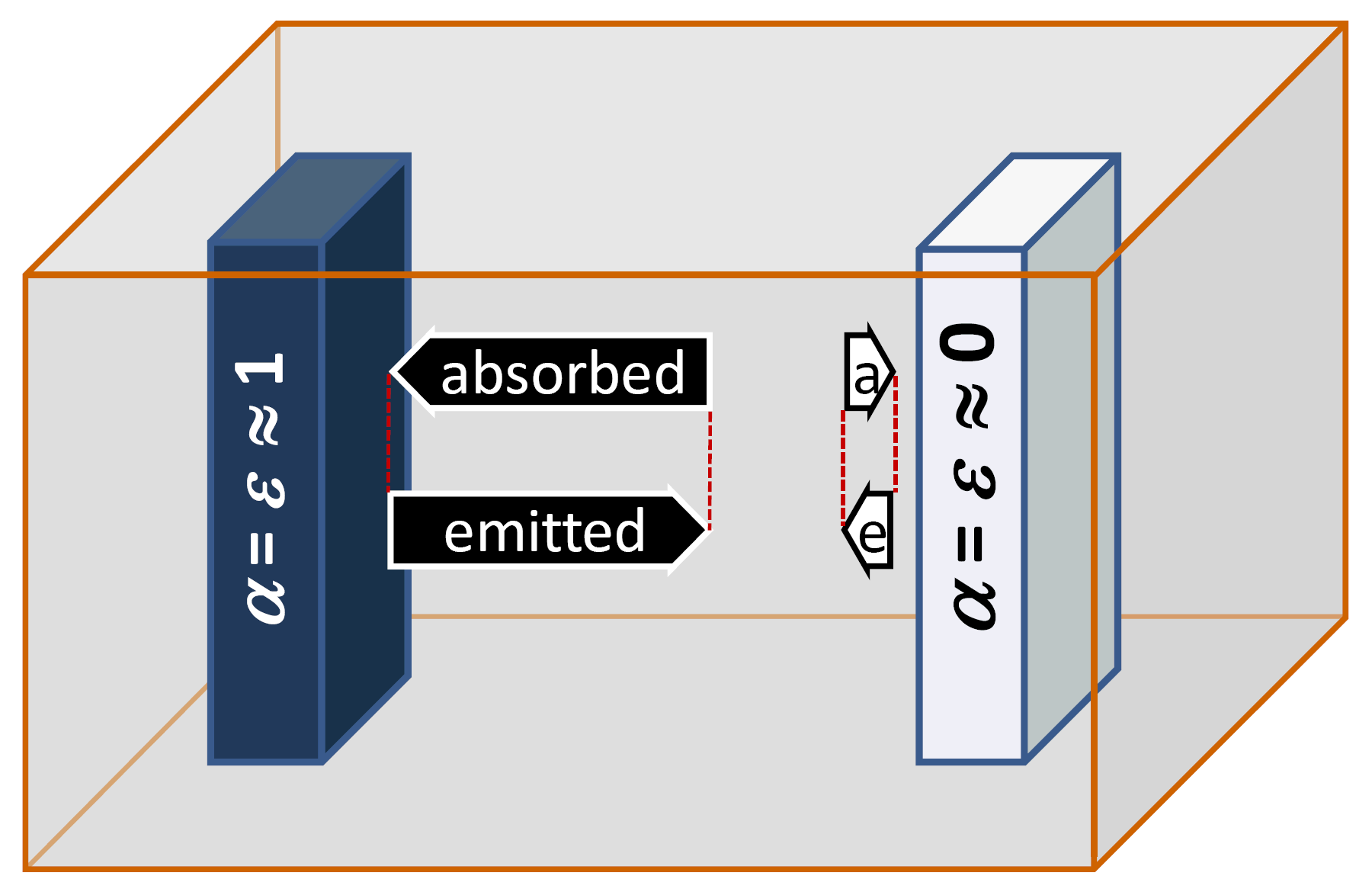
The white body is shown not completely free from absorption in the graph; 'ideal black' and 'ideal white' does not exist for real bodies.

As soon as a thermal equilibrium has been reached, the radiant powers of absorption and emission are equal to each other (dotted lines at the arrows). That is why the temperature would no longer change in a thermal equilibrium. A more detailed balancing and an exercise can be found in Supplement 2.1.

For the maximum degree of emission, this leads to an important result. On the previous page, based on Kirchhoff's examinations, it has been established that the thermal emission of black bodies reaches the highest values possible. $\epsilon =1$ thus is the degree of emission of black bodies. What follows is the defining equation:

The degree of absorption of an object can be different in different spectral ranges. This is valid for the degree of emission to the same extent. Bodies of which the absorption changes in function of the wavelength are called coloured bodies, in contrast to black, white and grey bodies of which the degree of absorption does not vary over the spectrum. Degrees of absorption and emission hence have to be applied to the same wavelengths:

This is Kirchhoff's radiation law.

Now we have enough knowledge to understand, how establish.