2. الإشعاع الحراري

The role of temperature: the Stefan-Boltzmann law

We are interested in the area under the Planck spectra of black bodies, that were discussed in the previous section. These areas obviously increase in size with increasing temperature of the emitter. The way in which this happens shall be found through determination of the area underneath the graphs.

The calculation of the area results from integration of the Planck graphs. Presuming the frequency depiction of the spectral energy density

u f = dU df = 8πh c 3 f 3 exp{ hf / kT }−1

By integration one obtains the energy density of all possible frequencies

U= ∫ f=0 ∞ u f  df= 8πh c 3 ∫ f=0 ∞ f 3 exp{ hf / kT }−1  df

Calculating the integral may be slightly difficult. The procedure is shown in Supplement 2.3. The result is:

U= 8 π 5 k 4 15 c 3 h 3 T 4

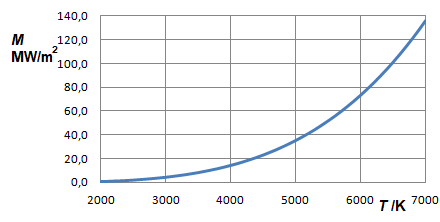
The specific emission M given in W/m² of a black body, for example the radiative power coming out of a cavity radiator's opening, is in most cases more meaningful for practical application than the energy density in (Ws)/m³ resp. J/m³ on the inside of the cavity. The relation is:

M= c 4 U

The result is the Stefan-Boltzmann law:

M= 2 π 5 k 4 15 c 2 h 3 T 4 =σ T 4
المعادلات ↓

With h=6.6⋅ 10 −34 Js , k=1.38⋅ 10 −23 J/K and c=3⋅ 10 8 m/s the Stefan-Boltzmann constant is obtained:

σ=5.670⋅ 10 −8 W m 2 K 4
Accordingly, the radiation increases disproportionately high with the fourth power of the temperature. Doubling the temperature for example from 300 K (room temperature) up to 600 K (327°C, melting point of plumb) results in an increase of radiation by 16 times!
Total radiation for 2000 - 7000 K Total radiation for 0 - 2200 K
Total radiation for 2000 - 7000 K
Total radiation M of black bodies. Left: In MW/m² at temperatures between 2000 and 7000 K. The radiating solar surface has a temperature of about 5800 K. Right: In kW/m² at temperatures between 0 and 2200 K. 300 K corresponds approximately to room temperature.
Source: Rainer Reuter, University of Oldenburg, Germany.