Supplement 1.8: Lambert emitters, cosine emitters      (4/4)

Further examples      ...Continued from previous page

Spherical luminaires

Spherical luminaires made of frosted glass or matt plastic, which are often used at home and outdoors, can be good Lambertian radiators. In the example on the previous page, we saw that the intensity from frosted glass does not depend on the angle of the glass. This therefore also applies to curved or spherical glass surfaces.

This property is clearly demonstrated in the photo on the left: the luminaire appears to be almost equally bright across its entire surface, regardless of the angle. Since the radiant intensity of the luminaire is the same in all directions, apart from deviations caused by the mechanical mounting, this is an isotropic emitter.

This is not the case with the luminaire in the right-hand image. Instead, there is a very bright central area. The outer areas are significantly darker. The luminaire is therefore not a Lambertian or cosine-distribution luminaire.

Luminaires with flat or only slightly curved frosted glass can also exhibit both characteristics. This also applies to the lamps used in the luminaires, which are often available with a frosted glass or plastic housing.

The darkening of the sun's limb

Limb darkening of the sun. A large sunspot can be seen at the bottom left.
Source: NASA Marshall Space Flight Center, USA

Now one might ask whether the Sun is a good or bad cosine spherical light source. If we average across the turbulent structures of the luminous photosphere, we obtain the image shown on the right, in which a clear darkening can be observed from the centre towards the limb.

The darkening at the edges is caused by the absorption and scattering of radiation from the photosphere in the higher, colder layers of the solar atmosphere. These losses depend on the wavelength; the effect is significantly higher in UV and blue than in red and IR.

A model of limb darkening was presented by Jeremy Tatum in the textbook Stellar Atmospheres, which describes the radiant intensity $I$ as a function of the distance r from the centre of the solar disc:

The parameter u is the limb darkening coefficient, with values of 0.56 at 600 nm (orange) and 0.95 at 320 nm (UV). a is the radius of the solar disc. Setting a=1 and normalising the centre distance r to the maximum value 1 yields the following curves.

Solutions to the equation shown above with (from bottom to top) u=1.0 - 0.8 - 0.6 - 0.4 - 0.2 - 0.0. For u=1.0, the result is a semicircle; for u=0.0, it is the upper edge of the graph.
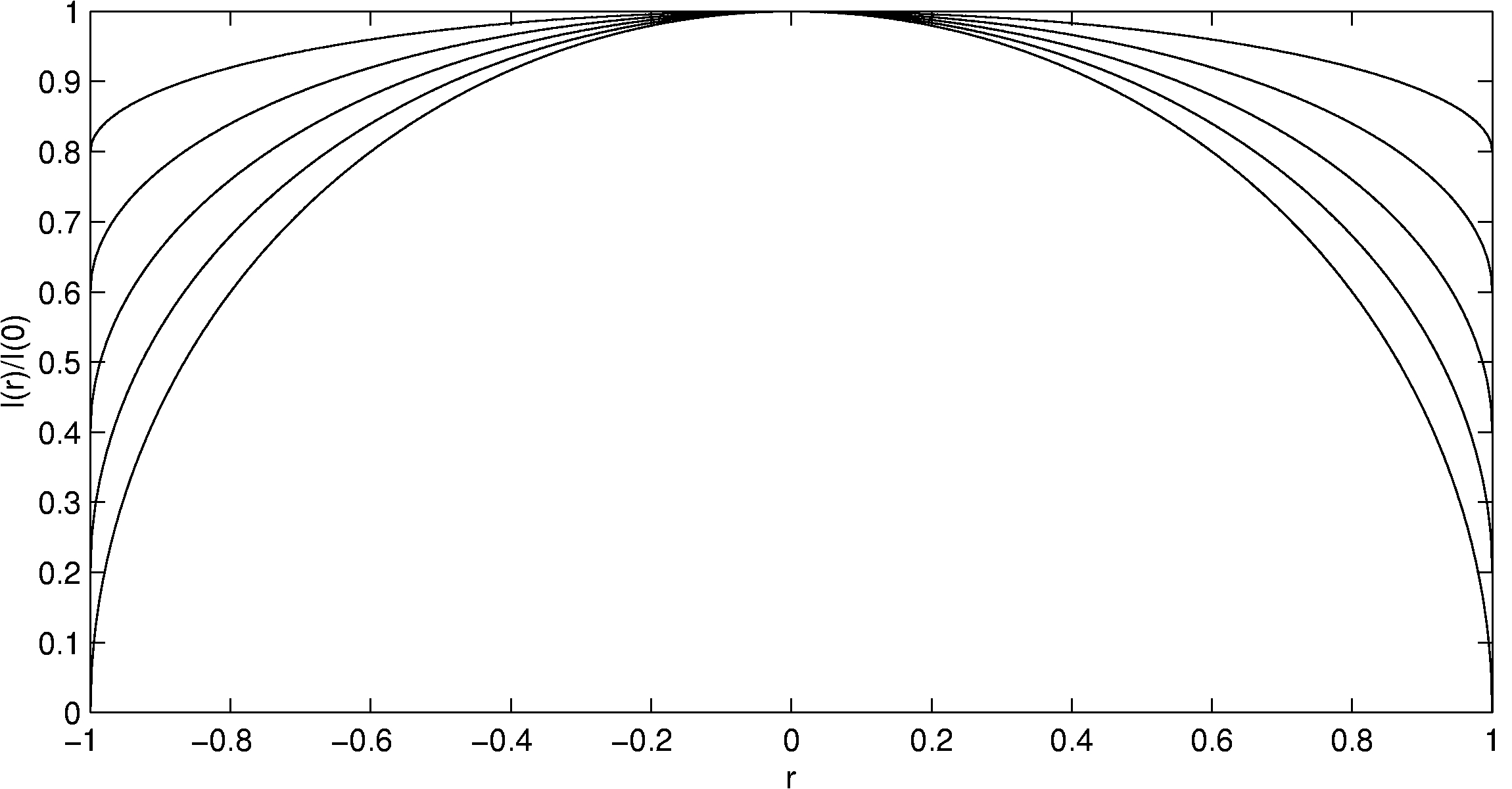
Source: Jeremy Tatum: Stellar Atmospheres, Chapter 6.