4. Classification par la distance minimum

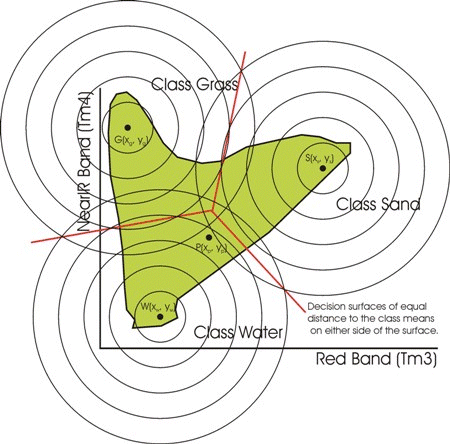
Considérons d'abords des données en 2-D (x,y). Avec la classification par distance minimum, les distances euclidiennes (E D) entre les valeurs des pixels (xp,yp) et les valeurs moyennes des classes sont calculées. Chaque pixel est associé à la classe par rapport à laquelle sa distance euclidienne est la plus faible. Il est aussi possible de fixer un critère de distance maximum, afin qu'un pixel se trouvant à une distance euclidienne supérieure à ce seuil par rapport à une moyenne de classe ne puisse pas être assigné à cette classe.

Information complémentaire sur les distances euclidiennes : ↓
Zoom Sign
Three classes, their Euclidean Distances and their Minimum Distance Decision Surfaces
Trois classes, leurs distances euclidiennes et leurs surfaces de décision par distance minimum
Zoom Sign
Skagen area
Image de Skagen, aires d'entrainement et classification par distance minimum.

Donc, pour les trois classes, on calcule les distances :

E D 2  =  ( x p − x g ) 2 + ( y p − y g ) 2 E D 2  =  ( x p − x s ) 2 + ( y p − y s ) 2 E D 2  =  ( x p − x w ) 2 + ( y p − y w ) 2

Ensuite, on assigne chaque pixel à la classe dont la moyenne se trouve à une distance euclidienne minimum, tant que cette distance est inférieure au seuil de distance maximum fixé.

La classification par distance minimum utilise des classes considérées comme ayant une corrélation nulle, et ayant toutes les mêmes valeurs de variance. C'est donc en fait un cas particulier de la classification par maximum de vraisemblance, que nous verrons au chapitre suivant.