2. Orbits and Parameters of GPS Satellites

The current GPS in space is made up of at least 24 satellites. GPS satellites are located at a height of 20,200 km above the Earth and are moving on an almost circular path along the Earth's central orbit.

A GPS satellite.

The velocity or speed as well as the time of revolution of a GPS satellite can be derived out of the information giving the distance between the Earth and the satellite. The forces that work on a satellite revolving on a circular orbit around the Earth are Gravitation

F_{G} = \frac{γ \cdot M \cdot m}{r^{2}}

and Centrifugal force

F_{Z} = \frac{M \cdot v^{2}}{r}

Because these forces compensate and balance each other, the satellite is able to maintain its circular motion around the Earth.

Specifically,

γ=6.67·10^-11m³(kg s²)^-1 is the gravitational constant,
M=5.976·10²⁴ kg is the Earth's mass,
m is the satellite's mass, and
r is the distance between the Earth's midpoint and the satellite.

The Earth's radius is r_E=6371 km .

Question 1
Using the given values F_G=F_Z, derive an equation for the satellite's velocity v with reference to its distance from the Earth's midpoint (or the radius of the circular path).

Answer ↓

By converting the given F_G=F_Z, we derive an equation which can be used to determine the velocity v on a cicular path

v = \sqrt{\frac{γ \cdot M}{r}}

r=26571 km is the distance of the satellite to the Earth's midpoint.

Question 2
Using the derived equation, compute the velocity of the satellite.

Answer ↓

Question 3
How long does a GPS satellite need to make one revolution?

Answer ↓

The time of revolution T of a circular path is the result of the quotient of the circumference r and the velocity v:

T = \frac{2 π \cdot r}{v}

r=26571 km is the distance of the satellite to the Earth's midpoint.
Using the above equation, we can compute the time needed by a GPS satellite to make one complete revolution. The result is: T=43104 s or 11h 58min.

Question 4
Derive an equation for computing the time of revolution T without reference to the velocity v.

Answer ↓

To express the time of revolution without reference to velocity, the equation for velocity may be used to replace the equation for time. The result is:

T = 2 π \sqrt{\frac{r^{3}}{γ \cdot M}}

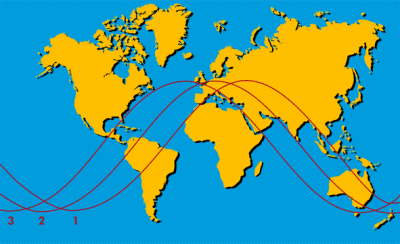
Therefore, a GPS satellite needs around 12 hours to make one complete revolution around the Earth, in other words, two times in one day. However, there is a very slight deviation of approximately two minutes per revolution which causes the same satellite to reach the same point approximately four minutes earlier each day. This means that the satellite's track shifts its position daily at approximately 1° westwards. The satellite's track or spoor is referred to as the geometrical locus of all points on the Earth's surface which correspond to the imaginary line connecting the satellite to the Earth's midpoint as it revolves on its orbit around the globe. The illustration below demonstrates the shifting of a sateliite's track.

Shifting of a satellite's track

Satellite Navigation with GPS

2. Orbits and Parameters of GPS Satellites