1. Global Positioning through Trilateration

Correcting the Clock Error

When using the trilateration method in global positioning, it is absolutely necessary that the receiver's clock and the satellite's clock are running synchronously.

GPS satellites are usually equipped with several atomic clocks.

Atomic clock at Physikalisch-technische Bundesanstalt in Braunschweig, Germany.
Source: Jörg Behrens, Wikimedia Commons

However, atomic clocks are too large and too heavy. Instead of an atomic clock, GPS receivers are equipped with crystal oscillators 1 to 2 cm in size. Their inaccuracy is around 10^-6, which is quite high for global positioning.

If we multiply the gear difference between atomic clocks and crystal oscillators with the speed of light c (which is the propagation speed of satellite signals), we obtain the error Δr, which is the result of the gear error of the crystal oscillators Δt:

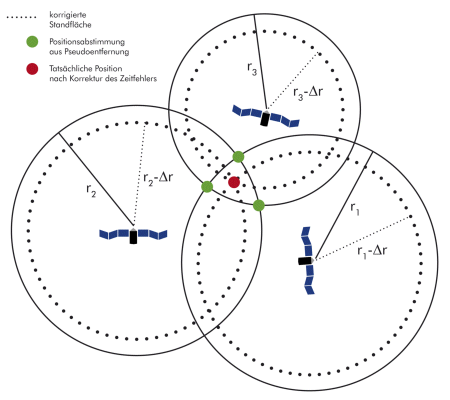
Therefore, the resulting distances are all afflicted with the same error Δr. This error leads to a rather inaccurate global positioning as shown in the illustration on the right.

Two-dimensional trilateration with three satellites and correction of the clock error (Here, three circles on a flat surface are used to illustrate a three-dimensional problem with four spheres.)

Problem
Two intersecting cicles have two common intersecting points. One of these points is definitely located on the Earth's surface, so that the other point is totally irrelevant. However, the third circle intersecting the first two does not intersect the common point where the other two circles meet.

Solution
To correct this inaccuracy, a fourth runtime measurement is taken in addition to the first three runtime measurements. This should reduce the inaccuracy of the clock. After correcting the pseudo-distances with the corresponding value Δr, an intersecting point for all three circles becomes visible. Therefore, accurate global positioning can only be possible with the use of four satellites.