1. Global Positioning through Trilateration

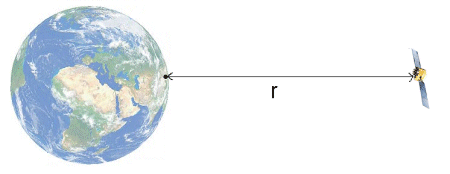
Distance between Transmitter and Receiver

GPS satellites are constantly transmitting data packages to GPS receivers on Earth. The signals contain information about time of transmission t_S, as well as the exact position x(t_S) of the satellite at the time of transmission.

The receiver is equipped with a clock which is synchronised with the satellite's clock. The receiver's clock records the time when the signal has been received t_E. Thus, we can compute the distance between the receiver and the satellite, as follows:

Having computed the distance between satellite and receiver, we may now assume that the receiver is located on the edge of an imaginary sphere with the radius r. The midpoint of this sphere is the position of the satellite x(t_S).

Think about it:

How many satellites are necessary to determine the exact position of the receiver?

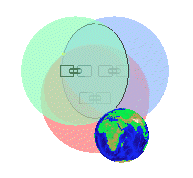
Three Intersecting Spheres

When two spheres intersect, their intersecting points form a circular line where the receiver must be located somewhere. When a third sphere intersects the first two spheres, this results in two possible positions of the receiver. Only one of these positions is located on Earth, so that the other position may be disregarded altogether.

Please click on the image:

The animation shows how three-dimensional global positioning works.

By using signals received from at least three satellites, we should be able to determine the position of the receiver on the Earth's surface.

Link to additional information for teachers and to three worksheets