2. Mit Zeitreihen arbeiten

Lineare Regressionsanalyse (1/3)

Wir untersuchen eine Methode zur Bestimmung von Ausgleichsgeraden am Beispiel der Zeitreihen zur Temperatur im Wattenmeer. Möglicherweise interessieren wir uns eher für die Temperaturen im Juli statt im Oktober, da wir im Sommer unsere Ferien am Meer verbringen. Die Juli-Daten sind unten dargestellt, links wie gemessen und über den Monat gemittelt, und rechts mit einigen geratenen Ausgleichsgeraden angenähert (zum Umschalten auf die Überschriften klicken). Welche Linie wäre wohl die beste Näherung?

Wassertemperaturen im Juli ...und geratene Ausgleichsgeraden

Der Einfachheit halber ändern wir die Variablen vom Jahr zu x und von der Temperatur zu y, und setzen x=1 am 1. Januar 2003. Der Juli ist der siebte Monat im Jahr, daher liegt der erste Datenpunkt im Diagramm bei $x=\left(1+(7/12)\right)=\mathrm{1,58}$, und so weiter. Aus der Tabelle der Wattdaten entnehmen wir die Wassertemperaturen im Juli 2003 bis 2008:

Das gleiche Diagramm wie oben links, aber in x/y-Koordinaten. Die Datenpunkte sind P(x_i,y_i), mit i=1, ... , 6.

Es gibt in der analytischen Geometrie mehrere Möglichkeiten zur Berechnung von Linien. Man könnte zwei Punkte suchen, die auf der Geraden liegen, und die Gerade durch diese Punkte bestimmen; dies ist die Zwei-Punkte-Form der Geradengleichung. In unserem Fall bietet es sich an, einen Punkt auf der Gerade und ihre Steigung zu verwenden; dies ist die Punkt-Steigungs-Form. Wir werden diese Form zur Berechnung der Ausgleichsgerade anwenden.

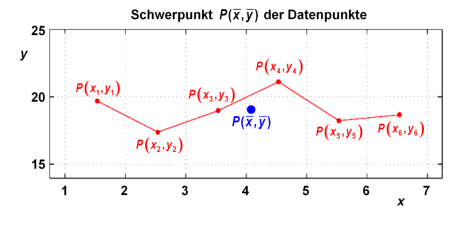
Schritt 1: Der Schwerpunkt

Der Schwerpunkt $P(\overline{x},\overline{y})$ der Daten liegt auf der Ausgleichsgeraden. Er kann aus dem arithmetischen Mittel der x_i und y_i-Werte der Datenpunkte bestimmt werden, siehe Ergänzung 1 für eine ausführliche Darstellung. Sei n eine ganze Zahl, die die Anzahl der Datenpunkte angibt; in unserem Fall ist n=6. Es folgt:

Der Schwerpunkt $P(\overline{x},\overline{y})$ der Datenpunkte, mit $\overline{x}=\mathrm{4,08}$ und $\overline{y}=\mathrm{19,01}$.

Schritt 2: Die Steigung

Die Abstände der Datenpunkte zu ihrer Ausgleichsgeraden sollen so klein wie möglich sein. Wie lassen sich diese Abstände definieren? Die beiden folgenden Abbildungen erläutern zwei mögliche Ansätze.

Abstände zur Geraden, Version 1 Abstände zur Geraden, Version 2

Version 2 ergäbe deutlich kompliziertere Gleichungen als Version 1, und - was hier nicht weiter gezeigt ist - die Ausgleichsgerade wäre von der Skalierung der x- und y-Achse abhängig. Man könnte auch eine dritte Version überlegen, bei der die horizontalen Abstände zwischen den Datenpunkten und den Punkten auf der Gerade betrachtet werden.

In unseren Berechnungen nutzen wir Version 1, d.h. die vertikalen Abstände zwischen den Daten und den Punkten auf der Geraden. Dieses Verfahren wird als lineare Regression bezüglich x bezeichnet.