1. Physical Basics
Radiation principles (2/2)
The Planck radiation law
In 1900, Max Planck introduced the concept of quantised properties of light, i.e., photons. This became the starting point of quantum theory. In the framework of classical physics and on the basis of electromagnetic waves it had not been possible to understand the physics of thermal radiation. Using the concept of photons, Planck derived an equation which describes the intensity and spectral shape of thermal radiation of an ideal black body emitter. Omitting some physical constants, it reads:
where λ ist the emission wavelength and T is the absolute temperature. It is h=6.68·10-34 Ws2 Planck’s constant, c the velocity of light, and k=1.38·10-23 Ws/K Boltzmann’s constant.
Obviously, emission spectra of ideal black bodies depend on their temperature only, and material properties do not interfer. Planck’s law therefore holds with solids, liquids and gases if their absorbance is α=1 (i.e., they absorb all incident radiation). Examples of Planck curves are shown in the graph on the right. Emission spectra of grey body emitters can be calculated using their spectral emission efficiency, i.e., ελMλ.
Wien's displacement law
Already in 1893 Wilhelm Wien derived an equation which allows to calculate the wavelength of maximum intensity λmax of a black body emission spectrum as a function of the temperature T:
where the value of the constant is 0.30 cm K. Hence, high temperatures correspond to maxima at low wavelengths and vice versa.
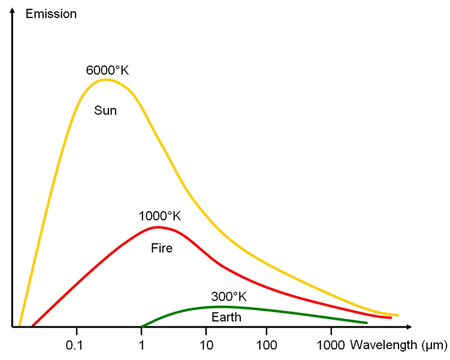
Source: ESA Eduspace with modifications
The sun with its high surface temperature of about 6.000 K emits visible light having a maximum at around λmax=0.5 µm. The Earth with an ambient temperature of 300 K emits predominantly in the mid infrared with a maximum around 10 µm; this spectral range is called the thermal infrared.
