Der Coriolis-Effekt
In welchem Bezugssystem sind Sie gerade?
Es sollte Sie nicht überraschen, dass eine Bewegung immer relativ zu einem bestimmten Bezugssystem stattfindet. Ein Beispiel: Während Sie in einem 100 km/h schnellen Zug sitzen und in Ruhe ein Buch lesen, bleibt das Buch in Bezug zu Ihnen unbeweglich auf der Stelle (d.h. im gleichen Bezugssystem innerhalb des Zuges); aus der Perspektive eines Beobachters außerhalb des Zuges jedoch bewegen Sie sich und das Buch mit der gleichen Geschwindigkeit wie der Zug, und zwar 100 km/h.
Nicht nur Bewegung hängt vom Bezugssystem ab, sondern auch die verschiedenen Kräfte, die man dabei spürt. Fährt der Zug also mit konstanter Geschwindigkeit, spüren Sie nichts. Beschleunigt sich der Zug, spüren Sie einen Ruck nach hinten. Bremst der Zug plötzlich ab, spüren Sie einen Ruck nach vorn. Fährt der Zug in eine Kurve, spüren Sie ein deutliches Ziehen nach Außen, die sogenannte Zentrifugalkraft. Um diesen Kräften standhalten zu können, müssen Bahngleise sehr stabil gebaut sein. Andernfalls könnte der Zug entgleisen (!), es soll aber schlimmstenfalls nur eine Wasserflasche auf Ihrem Tisch umkippen, wenn der Zug zu schnell in die Kurve fährt.
Die Kräfte, die man spürt, wenn der Zug beschleunigt, bremst oder in eine Kurve fährt, werden Scheinkräfte genannt – nur die Zugpassagiere können sie spüren. In anderen Worten, sie existieren nur in dem Bezugssystem des fahrenden Zuges. Sie sind jedoch wichtig, um die Ereignisse aus der Perspektive eines Beobachters zu erklären – andernfalls könnte man zum Beispiel, für das Umkippen der Wasserflasche keine Erklärung liefern. Jedesmal, wenn eine Bewegung untersucht wird, muss die Erklärung innerhalb eines Bezugsystems formuliert werden.
Die rotierende Erde als Bezugssystem
Wenn Meteorologen und Meeresforscher die Atmosphäre und die Ozeane unseres Planeten untersuchen, benötigen sie auch einen Bezugssystem. Logischerweise wird dafür ein Objekt genommen, das selbst mit der Erde rotiert und in dessen Perspektive die Erde als unbeweglich erscheint. Dies kann man mit der Perspektive einer auf der Erdoberfläche stehenden Person vergleichen (im Gegensatz zu der Perspektive eines Außerirdischen, der die Erde aus dem Weltall beobachtet!) Es ist die natürlichste Vorgehensweise, die Erde als unbeweglich zu betrachten.
Viele Bewegungen, die wir in unserem Alltag erleben, wie das Schwingen einer Pendeluhr, der Lauf einer Billiardkugel, oder die Flugbahn eines Fliegers, können in diesem Bezugssystem mit ziemlicher Genauigkeit ohne Zuhilfenahme fiktiver Kräfte formuliert werden. Betrachten wir jedoch großräumige Bewegungen (in der Größenordnung von hunderten bis tausenden von Kilometern, wie die Bewegung von Wind und Strömung), gibt es einige Merkwürdigkeiten, die nur durch Zuhilfenahme einer fiktiven Kraft, die von der Erddrehung ausgelöst wird, erklärt werden können. Diese Kraft ist die Coriolis-Kraft.

Die Coriolis-Kraft - Erklärung durch ein Karussell
Nehmen wir ein einfaches Beispiel, um die Corioliskraft zu erklären: Stellen Sie sich vor, Sie sitzen gerade auf einem rotierenden Karussell (es macht alle paar Sekunden eine ganze Umdrehung) und werfen dabei einen Ball in die Waagerechte. Aus der Perspektive eines externen Beobachters (also jemand, der nicht mit dem Karussell fährt) bewegt sich der Ball auf einer geraden Linie nach vorne. Aus Ihrer eigenen Perspektive jedoch (im Bezugssystem innerhalb des Karussells) bewegt sich der Ball auf einer Kurve. Dreht sich das Karussell gegen den Uhrzeigersinn, sehen Sie den Ball Richtung rechts fliegen, so wie im Film oben.
Die Kurve in der Flugbahn des Balles kommt durch den Coriolis-Effekt zustande.
In Ihrem (rotierenden) Bezugssystem, benötigen Sie eine zusätzliche Kraft, um das Ereignis zu erklären. Diese fiktive Kraft ist bekannt als die Coriolis-Kraft.
Die Coriolis-Kraft in atmosphärischen und ozeanischen Bewegungen
Dauer, Umfang und Geschwindigkeit einer Bewegung sind wichtig bei der Entscheidung, ob der Coriolis-Effekt berücksichtigt werden muss oder nicht. Als erstes müssen wir uns merken, das die Coriolis-Kraft nur für ein Objekt azftritt, das sich innerhalb des rotierenden Bezugssystems bewegt, d.h. eine Geschwindigkeit relativ zum Bezugssystem aufweist. Wie in unserem Beispiel oben dreht sich die Erde wie ein Karussell, aber viel, viel langsamer. Das bedeutet, dass der Corioli-Effekt der Erdrotation nur für großräumige Bewegungen (weiter als nur mehrere Kilometer), so wie bei Strömungen und atmosphärischen Turbulenzen der Fall ist, eine Rolle spielt.
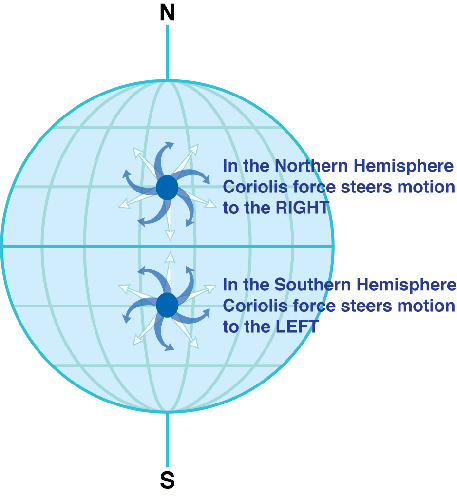
Die Coriolis-Kraft bewirkt, dass die Bewegung auf der Nordhalbkugel nach Rechts und auf der Südhalbkugel nach links abgelenkt wird. Am Äquator tritt kein Coriolis-Effekt auf.