7. Stochastische und deterministische Modelle (2/2)
Die Ursache dafür ist, dass die Anziehungskraft zwischen Erde und Mond nicht ganz ausreicht, um den Mond in einer fixen Umlaufbahn zu halten. Bei zunehmendem Abstand zwischen Mond und Erde nimmt die Gravitation ab, weshalb sich der Abstand zwischen den beiden unter sonst gleich bleibenden Bedingungen schneller vergrößert. In Wirklichkeit bleibt aber nicht alles andere gleich, die Geschwindigkeit des Mondes nimmt ab und die Zentrifugalkraft wird kleiner.
Ein anderer Typ deterministischer Modelle hat mit Tierpopulationen zu tun. Ersten Modellen des Populationswachstums lag die Idee des exponentiellen Wachstums zugrunde, das heißt dass die Zunahme der Population in einem Zeitabschnitt eine Funktion der Größe der Population zu diesem Zeitpunkt und der Wachstumsrate der Population ist.
Nt = N0 · Rt
dabei ist N0 die Anfangspopulation, N1 ist die erste Generation, R ist gleich 1,0 plus der Wachstumsrate und Nt steht für die t-te Generation.
Nehmen wir die Zellteilung als Beispiel. Wenn sich jede Zelle in jeder Generation zweiteilt, dann ist R = 2. Gibt es in der ersten Generation eine Zelle, so haben wir in der zweiten zwei Zellen, in der dritten vier, in der vierten acht Zellen und so weiter. Hierbei handelt es sich um ein exponentielles Wachstum.
Versuchsdaten haben jedoch ergeben, dass dies zwar unter manchen Bedingungen zutrifft, aber nicht immer der Fall ist. Diese Beobachtung führte zu der Annahme, dass Populationen in ihrem Wachstum beschränkt werden, sobald sie eine bestimmte Größe erreichen. Die Wachstumsrate kann beispielsweise durch den verfügbaren Raum oder die vorhandene Nahrung reduziert werden. Diese Feststellung hat zu der Entwicklung neuer Wachstumsmodelle geführt, die auf der logistischen Wachstumskurve basieren.
wobei K die Obergrenze des Populationswachstums darstellt, die oft als Trägerkapazität bezeichnet wird, und ro = R - 1.
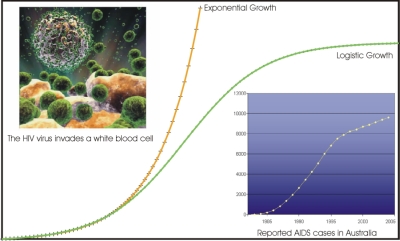
Quelle: Murray Bourne, 1997-2009
Das AIDS-Virus wurde von 100 Personen in eine Stadt mit einer Einwohnerzahl von 50 000 Personen gebracht. Nach 10 Wochen wurde festgestellt, dass 1 000 Personen infiziert waren. Wie lange dauert es unter der Annahme, dass die Epidemie einer logistischen Kurve folgt, bis die Hälfte der Einwohner von dem Virus betroffen ist?
Wir wissen also, dass t = 10 Wochen ist. Verwenden Sie nun die obenstehende Gleichung mit den gegebenen Daten und finden sie die Wachstumsrate ro = 0,23208. Setzen Sie diese Wachstumsrate in die Gleichung ein, und sie kommen zu dem Ergebnis, dass die Hälfte der Population nach 26,8 oder ca. 27 Wochen infiziert sein wird.
Fragen
- Wie groß ist die Anziehungskraft zwischen Ihnen und der Erde? Sie brauchen das nicht auszurechnen, täten Sie dies, käme genau ihr eigenes Körpergewicht heraus. Ihr Gewicht ist ein Maß dieser Kraft.
- Wieviel wiegen Sie auf dem Mond? Beantworten Sie diese Frage zunächst unter Anwendung des Gravitationsgesetzes,
indem Sie dieses in ein Verhältnis zwischen der Schwerkraft der Erde und derjenigen des Mondes umwandeln.
Vereinfachen Sie dieses Verhältnis um folgende Gleichung zu erhalten:
Um das Verhältnis zu bestimmen, nutzen Sie die Masse des Mondes von 0,73483·1023 kg und seinen Radius von 1 738 km sowie die Masse der Erde von 59,74·1023 kg mit dem Radius 6 371 km. Wissen wir das Gewicht einer Person auf der Erde, so erlaubt uns dies die Berechnung ihres Gewichts auf dem Mond. Überprüfen Sie ihre Antwort, indem Sie auf dieser Seite nachsehen.
