2. Die Methode der kleinsten Quadrate (2/2)
In dieser Gleichung steht das N für N Gleichungen aus Beobachtungen, da wir die Quadrate der Residuen aufsummieren. Ordnen wir die Gleichungen in zwei Matrizen an, wird die Lösung relativ einfach.
wobei , und für die drei Matrizen oben stehen. Wenn wir beide Seiten mit der Transponierten der ersten Matrix multiplizieren, erhalten wir
oder , diese werden als Normalgleichungen bezeichnet. Sie können ganz einfach zeigen, dass die Matrixgleichung die selbe Form besitzt wie die vorherigen Gleichungen.
In der Gleichung ist die inverse Matrix der Matrix .
Bei der einfachen linearen Regression ist die Matrix eine (2,2)-Matrix, ist eine (2,1)-Matrix und eine (2,1)-Matrix, sodass die Normalgleichungen direkt gelöst werden können, ohne dass die Matrix invertiert werden müsste. Die beiden Normalgleichungen sind
Hier können wir nach b1 und b0 auflösen.
Dabei ergibt sich
ŷ ist nicht der tatsächliche y-Wert, sondern der Schätzwert für y. Von dem y-Wert weicht er um die Größe des Residuums des beobachteten Wertepaares ab.
Sie können den Datensatz mit den zusammenpassenden Datenpaaren des Ratio Vegetation Index (RVI) und des Grünem Blattflächenindex (GLAI) für Winterweizen und Sommergerste in ein Tabellenblatt importieren und diese Gleichungen nutzen, indem Sie die Summen und die Summen der Produkte in einzelnen Feldern in Ihrem Tabellenblatt bilden und dann nach den beiden Unbekannten auflösen. Nachdem Sie dies für eine Getreidesorte getan haben, können Sie die Zellen einfach kopieren und bei der anderen Getreidesorte genauso vorgehen.
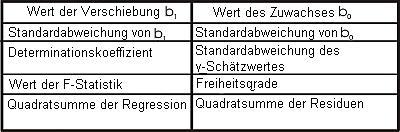
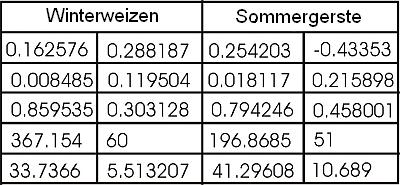
Probieren Sie nun die Funktion RGP in Excel aus. Markieren Sie einen leeren Bereich mit zwei Spalten und fünf Zeilen, um RGP zu verwenden. Fügen Sie die Funktion RGP hier ein, indem Sie zuerst die y-Werte (GLAI) und dann die x-Werte (RVI) angeben und dann auf 'Ok' gehen und auch für die anderen beiden Eingaben 'Ok' wählen. Drücken Sie nun gleichzeitig Strg-Shift-Enter, damit die Funktion die zehn von Ihnen gewählten Felder ausfüllt. In der Hilfe zu der Funktion RGP wird erklärt, was die Werte bedeuten. Ihre Bedeutung ist auch in der Tabelle auf der linken Seite zusammengefasst.
Für die beiden gegebenen Datensätze sollten Sie die in der untenstehenden Tabelle angegebenen Werte erhalten.
Aufgaben
- Holen Sie sich den im vorigen Kapitel erwähnten Datensatz und öffnen Sie ihn in einem Tabellenblatt oder verwenden Sie gegebenenfalls das bereits von Ihnen erstellte Tabellenblatt. Führen Sie eine lineare Regression durch, indem Sie zunächst das SUMMMENPRODUKT der Größen X2 und XY bilden und dann X und Y summieren. Achten Sie darauf, dass Sie die richtigen Spalten für X und Y markieren. Berechnen Sie anschließend die beiden Regressionsparameter, indem Sie von den auf dieser Seite angegebenen Gleichungen die entsprechenden Gleichungen verwenden.
- Nutzen Sie für die gleiche Aufgabe die Funktion RGP. Die Werte für die beiden Parameter finden Sie in den von RGP ausgegebenen Ergebnissen, das Ergebnis enthält jedoch auch noch viele weitere Dinge, auf die wir im nächsten Kapitel noch eingehen möchten.
- Markieren Sie auf dem Graphen die einem Datensatz zugehörigen Datenpunkte. Ein Pop-up-Menü sollte jetzt erscheinen; wählen Sie in diesem Menü 'Trendlinie hinzufügen', wobei Sie eine lineare Trendlinie verwenden. Geben Sie außerdem an, dass die Geradengleichung und der Wert für R2 in dem Diagramm angezeigt werden sollen.
- Nutzen Sie die von Ihnen abgeleiteten Regressionsgleichungen, um die Residuen jeder Beobachtung in den beiden Datensätzen zu berechnen. Erstellen Sie einen Plot der Residuen und berechnen Sie Mittelwert und Varianz der Residuen. Was fällt Ihnen an Mittelwert und Varianz auf?