14. Solution of Exercises in Chapter 8
3. The Telescope
- Defining the solid angle with an aperture
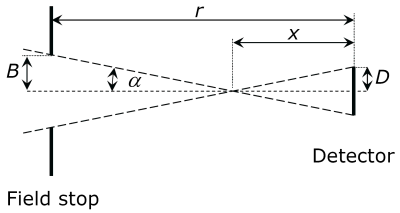
The simplest way to limit the visual field of a detector is by using an aperture.
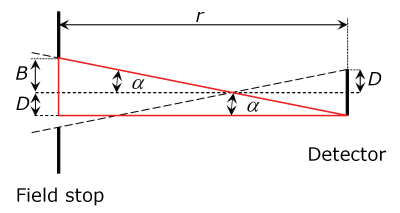
A detector with an aperture to limit its visual field.Detector and aperture are at a distance r from one another. The detector's radius is D, the aperture's radius is B. α corresponds to the biggest possible acceptance angle in half.
Question:
Using the given geometric relations, derive an equation for the acceptance angle α as a function of B and D.Hint: Find a right-angled triangle with the angle α and the radii B and D.
Answer:
Geometry of the detector with aperture for limiting the acceptance angle. - Defining the solid angle with lens and aperture
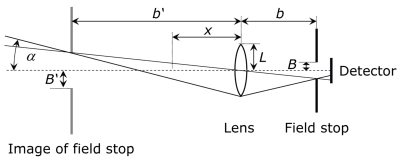
The efficiency of a detector with aperture is very poor. Much higher efficiencies can be achieved when adding a collecting lens to the set-up.
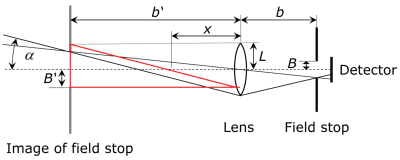
A detector with a collecting lens and an aperture for limiting the field of view.The maximum acceptance angle α is defined by the lens (with radius L and focal length f) and the aperture at distance b. The sensitive area of the detector behind the aperture is assumed to be sufficientlly large so that the detector does not limit the path of rays. The acceptance angle α follows from the image of the aperture B' at a distance b' from the lens.
Question:
a) Using the given geometric relations again and also the lens equations, derive an equation for the acceptance angle α as a function of L, B, b and f.
b) In which way can the result be simplified with b=f, i.e., with the aperture at the focal distance from the lens?Hint: Again, find a right-angled triangle with the angle α and the quantities L, B' and b'. Use the lens equations to convert the equation from B' and b' to B and b.
Answer:
Geometry of the detector with collecting lens and an aperture to limit its visual field.a)
b)
