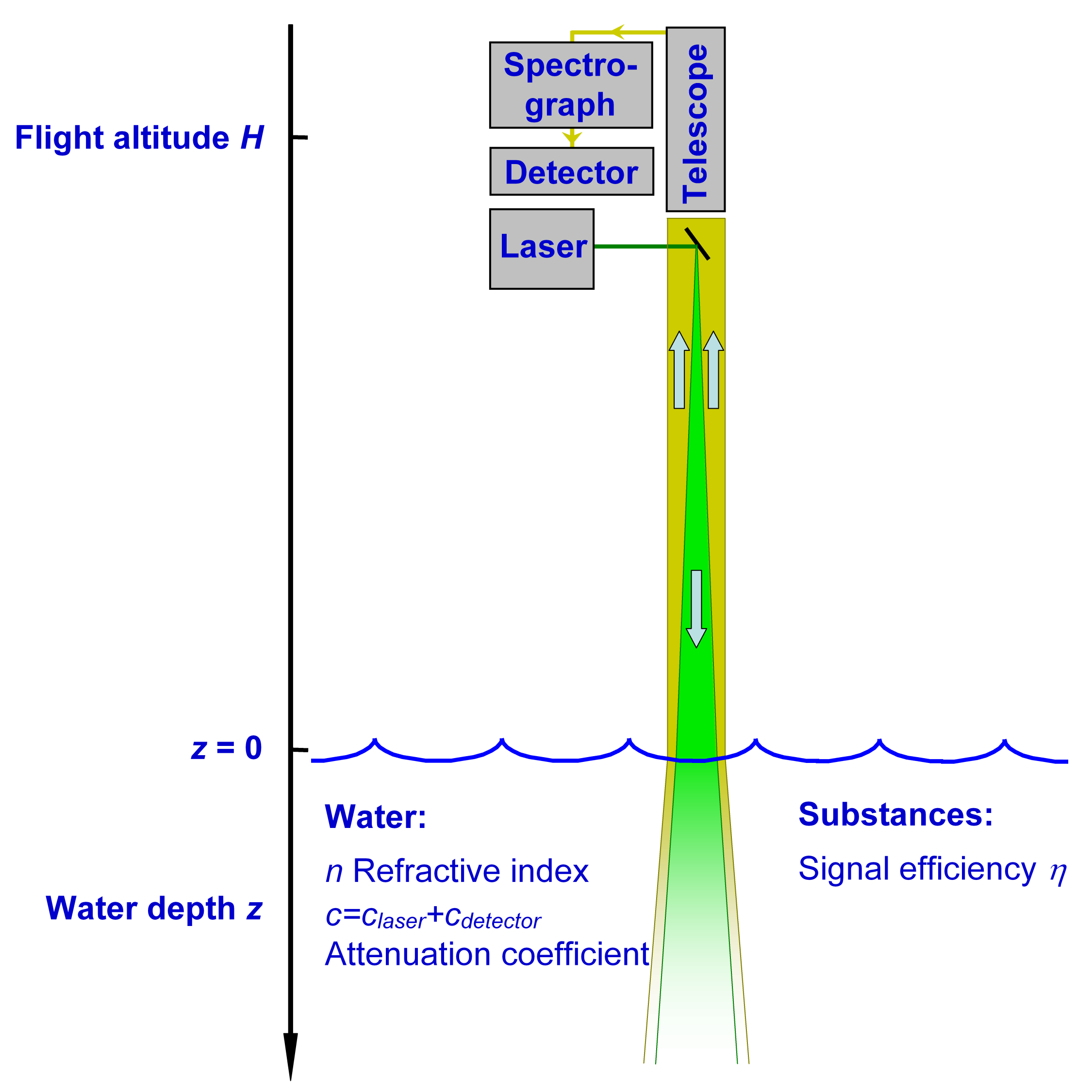
Supplement 7.1: The Hydrographic Lidar Equation (1/3)

The equation

We consider a lidar installed in an aircraft (or another airborne platform) and operated at a flight altitude H over water.

Elements of a hydrographic lidar aboard aircraft over water.

The laser emits light pulses having a wavelength λ_laser towards the water surface. The vertical coordinate is z, with z=0 at the water surface and z positive downwards.

In the water column the laser light is attenuated according to Lambert’s law by absorption and scattering. Hence, at a given depth z there is only a fraction exp(-c_laserz) of the laser intensity at the water surface. The quantity c_laser is the attenuation coefficient of light at the laser wavelength. If the distribution of absorbing and scattering substances is depth dependent then the attenuatiuon coefficient is also depth dependent, and at depth z one finds the fraction

exp (- \int_{z' = 0}^{z} c_{l a s e r} (z') d z')

of the laser light (z' is the variable of integration, z is the considered depth).

A signal produced at depth z (fluorescence, scattering) is also attenuated along its path towards the water surface by absorption and scattering. This depends on the attenuation coefficient c_detector if the detector measures a signal at a wavelength λ_detector, defined by the settings of the spectrograph. The light attenuation between the water surface and the depth z and back to the water surface is then:

exp (- \int_{z' = 0}^{z} (c_{l a s e r} (z') + c_{det e c t o r} (z')) d z')

To simplify the equations, the attenuation coefficients are combined according to c=c_laser+c_detector in the following. The light propagation in air is assumed to be free of intensity losses.

Substances in the water column are characterised by the signal efficiency η, given by molecular optical properties (e.g., the specific fluorescence efficiency) and the concentration. The optical power measured by the lidar detector from an infinite depth interval dz at depth z is then:

d P \propto η \frac{exp (- \int_{z' = 0}^{z} c (z') d z')}{{(z + n H)}^{2}} d z

The quantity (z+nH)² arises from the photometric law of distance: the brightness of a light source gets lower by the inverse square of the distance. The refractive index n of water takes into account refraction at the water surface. The influence of waves on the raypath are not considered here.

This is the hydrographic lidar equation. Specific instrumental properties of the lidar such as the power of the laser beam, the telescope aperture etc. are not considered, and therefore the relation is given as a proportionality.

Solving the equation

A lidar signal originating from a finite water layer at a depth between z₁ and z₂ is derived from integration:

P_{z_{1} \to z_{2}} \propto exp (- \int_{0}^{z_{1}} c d z) \cdot \int_{z_{1}}^{z_{2}} η \frac{exp (- \int_{z_{1}}^{z} c d z')}{{(z + n H)}^{2}} d z

The second integral is denoted by $Φ$ :

Φ = \int_{z_{1}}^{z_{2}} η \frac{exp (- \int_{z_{1}}^{z} c d z')}{{(z + n H)}^{2}} d z

With w=(z+nH)/nH and assuming c and η to be constant betweenn z₁ and z₂, the integral over this layer is written as

Φ = η \frac{exp (n H c w_{1})}{n H} \int_{w_{1}}^{w_{2}} \frac{exp - (n H c w)}{w^{2}} d w

With the substitution

d w = - \frac{1}{n H c + \frac{2}{w}} \frac{w^{2}}{exp - (n H c w)} d \frac{exp - (n H c w)}{w^{2}}

and approximating nHc»2/w which is equivalent to c»2/(z+nH) and will be valid for all practical cases, the integration is straightforward:

Φ = \frac{η}{c} \frac{1}{{(n H)}^{2}} (\frac{1}{w_{1}^{2}} - \frac{exp - (n H c (w_{2} - w_{1}))}{w_{2}^{2}})

The lidar signal from the finite water layer between z₁ and z₂ then reads:

P_{z_{1} \to z_{2}} \propto exp (- \int_{0}^{z_{1}} c d z) \cdot \frac{η}{c} (\frac{1}{{(z_{1} + n H)}^{2}} - \frac{exp - (c (z_{2} - z_{1}))}{{(z_{2} + n H)}^{2}})

This relation is generally valid to calculate signals from a stratified water column. The relation between the time function $P (t)$ of the measured lidar signal and the depth function $P (z)$ above is given by the equation

z = c t / 2

which connects the elapsed time t of light propagation with the distance z; the factor 2 in the denominator is due to the fact that the light travels twice the distance z, forth and back. This requires however laser pulses having a pulse length $Δ t$ which is sufficiently short, at least shorter than the thickness of layers which shall be detected:

Δ t \leq \frac{2}{c} (z_{2} - z_{1})

Light in water propagates in a nanosecond time a distance of approx. 20 cm, and therefore a 1 ns laser pulse length corresponds to a 10 cm depth resolution; layers having this thickness can be traced in the measured signal.

Longer pulse lengths ’smear‘ thinner structures in a stratified water column. Mathematcally this is given by a so-called convolution of the system time response function of the lidar with a signal that could be measured with an infinitely short laser pulse; the latter can be calculated with a deconvolution of the true measured signal. This is discussed in detail in the literature.

On the next page we consider several special cases, which follow from a time integration of the detected signal over its entire duration. Information on stratified structures is lost by time integration, and one obtains averaged parameters from the upper water layers, e.g. the average attenuation coefficient. Laser fluorosensors measure time integrated signals, in contrast to time resolving lidars.

Remote Sensing Using Lasers

Supplement 7.1: The Hydrographic Lidar Equation (1/3)

The equation

Solving the equation