5. Exercises

2. Thermal Radiation

Supplement 2.1: Absorption, Emission and Reflection

Task: From imbalance to equilibrium

Two bodies in a thermal equilibrium within a cavity isolated from the environment. The arrows depict the radiant powers. The letters e, a and r stand for the emitted, absorbed and reflected radiation of the white body.

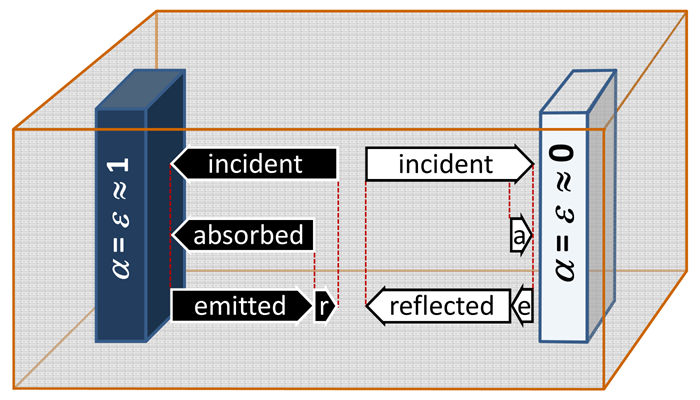
Outline as shown in the graph, in how far the length of the flashes would change in the following cases:

the black body is of a higher temperature than the white body
the white body is of a higher temperature than the black body.

Questions:

how does the length of the arrows change for the absorbed and the emitted radiation of both bodies?
what length of the arrows does result for the incoming such as the reflected radiation?
recognise how the tendency of approximation of the temperatures can arise.

Answer:

The situation is quite complex and confusing at a first glance. Sketches of radiation balances are hery helpful for an understanding. Some useful hints are given in the following. They focus on the initial conditions of two bodies in contact, where one body has a higher temperature and the other one has the temperature of the initial equilibrium.

a) the black body has higher temperature than the white one.

1: Black body: emitted and absorbed are stronger. White body: emitted remains the same, absorbed is stronger.
2: Black body: incident and reflected are stronger. White body: incident and reflected are stronger.
3: The emission of the white body remains the same, all other quantities increase; the balance for the white body is stronger than for the black body.

b) the white body has higher temperature than the black one.

1: Black body: emitted remains the same, absorbed is stronger. White body: emitted and absorbed are stronger.
2: Black body: incident and reflected are stronger. White body: incident and reflected are stronger.
3: the emission of the white body remains the same, all other quantities increase; the balance for the black body is stronger than for the white body.

Equations ↓

Supplement 2.6: Differentials and Derivatives

Task 1: partial derivatives and differentials

Please calculate the partial derivatives and the total differential of the following functions:

z = x^{3} y + x^{2} y^{2} + x y^{3}

z = x sin y - y sin x

Answers:

z = x^{3} y + x^{2} y^{2} + x y^{3}

The partial derivatives:

\frac{\partial z}{\partial x} = 3 x^{2} y + 2 x y^{2} + y^{3}

\frac{\partial z}{\partial y} = x^{3} + 2 x^{2} y + 3 x y^{2}

The differential:

d z = (3 x^{2} y + 2 x y^{2} + y^{3}) d x + (x^{3} + 2 x^{2} y + 3 x y^{2}) d y

z = x sin y - y sin x

The partial derivatives:

\frac{\partial z}{\partial x} = sin y - y cos x

\frac{\partial z}{\partial y} = x cos y - sin x

The differential:

d z = (sin y - y cos x) d x + (x cos y - sin x) d y

Task 2: total derivatives

Find the total derivative of

z = x^{2} + 3 x y + 5 y^{2}

where $x = sin t$ and $y = cos t$ .

Answer:

The partial derivatives:

\frac{\partial z}{\partial x} = 2 x + 3 y

\frac{\partial z}{\partial y} = 3 x + 10 y

Derivatives of the variables:

\frac{d x}{d t} = cos t

\frac{d y}{d t} = - sin t

The total differential:

\frac{d z}{d t} = (2 sin t + 3 cos t) cos t - (3 sin t + 10 cos t) sin t

Exercise 3: Partial derivative and total differential of a vector

The calculation rule for the differential applies not only to scalar functions, but also to vectors in the same way. We consider the vector $\vec{A} (x, y, z)$ :

d \vec{A} = \frac{\partial \vec{A}}{\partial x} d x + \frac{\partial \vec{A}}{\partial y} d y + \frac{\partial \vec{A}}{\partial z} d z

Please calculate the partial derivatives and the total differential of

\vec{A} = (x^{2} sin y, z^{2} cos y, - x y^{2})

Solution:

Based on the definition of the total differential:

\begin{array}{l} d \vec{A} = \frac{\partial \vec{A}}{\partial x} d x + \frac{\partial \vec{A}}{\partial y} d y + \frac{\partial \vec{A}}{\partial z} d z \\ = (2 x sin y,0, - y^{2}) d x + (x^{2} cos y, - z^{2} sin y, - 2 x y) d y \\ + (0,2 z cos y,0) d z \\ = (2 x sin y d x + x^{2} cos y d y, - z^{2} sin y d y 2 z cos y d z, - y^{2} d x - 2 x y d y) \end{array}

Alternatively, you can also calculate the total differential of each individual term of $\vec{A}$ directly:

\begin{matrix} d \vec{A} = (d (x^{2} sin y), d (z^{2} cos y), d (- x y^{2})) \\ = (2 x sin y d x + x^{2} cos y d y, - z^{2} sin y d y 2 z cos y d z, - y^{2} d x - 2 x y d y) \end{matrix}

Task 4: Temperature in space and time

The temperature may be given by the function

T = T_{o} + a x - b x y^{2} + c y z^{2} + d z t

with:
$T_{o}$ =20°C
$a$ =0.3°C/m
$b$ =0.02°C/m³
$c$ =0.1°C/m³
$d$ =0.01°C/(m·s)

a) What is the temperature like at the location $\vec{r}' = (x', y', z')$ = (10 m, 5 m, 2 m) at the time $t'$ = 100 s.

b) Calculate the partial derivatives of the temperature. What values do you obtain for the location $\vec{r}'$ and at the time $t'$ ?

c) Calculate the temperature difference $d T$ for the displacement
$d \vec{r} = (d x, d y, d z)$ = (1 m, 0.5 m, 0.5 m) with the time $d t$ = 2 s later.
(We treat the differentials for approximation as finite quantities)

d) What values does the temperature $T (\vec{r}' + d \vec{r}, t' + d t)$ take?

Answers:

a) $T (\vec{r}')$ = 22°C

b)	$\frac{\partial T}{\partial x} = a - b y$	${(\frac{\partial T}{\partial x})}_{\vec{r}', t'}$ = 0.2°C/m
	$\frac{\partial T}{\partial y} = - 2 b x y + c z^{2}$	${(\frac{\partial T}{\partial y})}_{\vec{r}', t'}$ = 0.4°C/m
	$\frac{\partial T}{\partial z} = 2 c y z + d t$	${(\frac{\partial T}{\partial z})}_{\vec{r}', t'}$ = 3°C/m
	$\frac{\partial T}{\partial t} = d z$	${(\frac{\partial T}{\partial t})}_{\vec{r}', t'}$ = 0.02°C/m

c) $d T$ = 1.94°C

d) $T (\vec{r}' + d \vec{r}, t' + d t)$ = 21.94°C

Task 5: Nabla operator and velocity vector

The Nabla operator can be linked to a vector, for example the velocity vector.

a) Depict the terms $\nabla \cdot \vec{v}$ and $\nabla \times \vec{v}$ ` in Cartesian coordinates. Are they scalars or vectors?

b) What is the meaning of these terms? What does the term $\vec{v} \cdot \nabla$ mean?

Answers:

\nabla \cdot \vec{v} = \frac{\partial u}{\partial x} + \frac{\partial v}{\partial y} + \frac{\partial w}{\partial z}

\nabla \times \vec{v} = | \begin{matrix} \vec{i} & \vec{j} & \vec{k} \\ \frac{\partial}{\partial x} & \frac{\partial}{\partial y} & \frac{\partial}{\partial z} \\ u & v & w \end{matrix} | = ((\frac{\partial w}{\partial y} - \frac{\partial v}{\partial z}), (\frac{\partial u}{\partial z} - \frac{\partial w}{\partial x}), (\frac{\partial v}{\partial x} - \frac{\partial u}{\partial y}))

with the unit vectors $\vec{i}$ , $\vec{j}$ and $\vec{k}$ in directions of the coordinate axes $x$ , $y$ and $z$ .

$\nabla \cdot \vec{v}$ is a scalar, $\nabla \times \vec{v}$ is a vector.

The term $\nabla \cdot \vec{v}$ is also called the divergence of the velocity and refers to sources or sinks of velocity. A positive balance denotes a source of velocity in the region, as given in an expanding gas for example. A negative balance depicts a compression of a gas. Keyword for further reading: Gauss' theorem.

The term $\nabla \times \vec{v}$ is also called the rotation of the velocity and refers to its vorticity. It is non-zero in the presence of shear flows, eddies and turbulences. Keyword for further reading: Stokes' theorem.

$\vec{v} \cdot \nabla$ is the multiplication of the velocity vector and the Nabla operator. Standing alone it does not have any meaning so far, The differential operator must be applied to another quantity, a scalar or a vector. See Supplement 2.6, page 3.