Supplement 4.3: Polarisation of Electromagnetic Waves, an Introduction

The first approach

On Page 2 of the section about electromagnetic waves we developed equations for the electric and the magnetic field of a plane monochromatic wave:

E (x, t) = E_{o} sin 2 π (\frac{x}{λ} - \frac{t}{T}) B (x, t) = B_{o} sin 2 π (\frac{x}{λ} - \frac{t}{T})

Due to the periodic behaviour of the sine function in $2 π$ , the equations show the periodicity with the wavelength λ and the period T. Instead of these quantities, other parameters which include the factor $2 π$ are useful since then the equations can be written much shorter. These are:

the wavenumber $k = \frac{2 π}{λ}$
the angular frequency $ω = \frac{2 π}{T} = 2 π f$

What means that:

E (x, t) = E_{o} sin (k x - ω t) B (x, t) = B_{o} sin (k x - ω t)

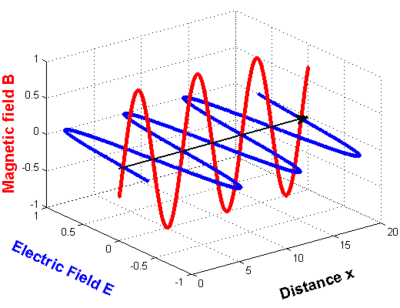
This is what the wave looks like in a graphics:

An electromagnetic wave propagating from left to right along the x axis. The curves show the peak positions of both field vectors, which stand perpendicular to the x axis (black arrow). Animation.

The oscillations of the electric and the magnetic field are obviously very regular for this wave. This is called a polarised wave. A wave is called unpolarised if the oscillations behave completely irregular. Waves can be partially polarised.
Only transverse waves - for example electromagnetic waves - may be polarised. Longitudinal waves - for example sound waves - are not polarised.

In the graphics shown above, nothing is said about the direction of the electric and the magnetic field (except from the fact that they stand perpendicularly to each other and to the direction of propagation): y- and z-coordinates are missing, in order to depict the direction of the field strength vectors.

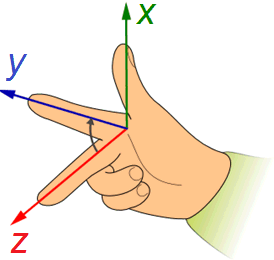
We now examine a wave, which propagates in x-direction in an three dimensional right handed $(x, y, z)$ coordinate system. Only the electric field is looked at; the results are valid for the orthogonally oscillating magnetic field as well.

Equations ↓

Left and right handed Cartesian coordinates.

The field vector $\vec{E}$ stands orthogonally on the direction of propagation x. It is split into components along directions y and z:

E_{y} = E_{y, o} sin (k x - ω t) E_{z} = E_{z, o} sin (k x - ω t + φ)

$E_{y, o}$ and $E_{z, o}$ are the amplitudes. The quantity $φ$ indicates the phase displacement between the two components. For a monochromatic wave, $φ$ is constant, both wave components thus are coherent.

The values of

E_{y, o}

E_{z, o}

and

φ

completely characterise the type of polarisation of a monochromatic wave: It can be linear, circular or elliptic.

The most important types of polarisation and their oscillation characteristics, $n$ is an entire number:

Condition	Type of polarisation
$E_{z, o} = 0$	linear along the y axis
$E_{y, o} = 0$	linear along the z axis
$φ = 2 n π, E_{y} = \frac{E_{y, o}}{E_{z, o}} E_{z}$	linear diagonally in the first and third quadrant of the y,z plane
$φ = (2 n + 1) π, E_{y} = - \frac{E_{y, o}}{E_{z, o}} E_{z}$	linear diagonally in the second and fourth quadrant of the y,z plane
$φ = (2 n - \frac{1}{2}) π, E_{y, o} = E_{z, o}$	right circular: The field vectors turn right (facing the wave). *Animation* of the turning vector heads, the E field is shown in blue, the B field in red.
$φ = (2 n + \frac{1}{2}) π, E_{y, o} = E_{z, o}$	left circular: The field vector turn left (facing the wave)
$φ = (2 n - \frac{1}{2}) π, E_{y, o} \neq E_{z, o}$	right elliptic: The field vectors turn right (facing the wave). *Animation* of the turning vector heads, the E field is shown in blue, the B field in red.
$φ = φ (t), E_{y, o} = E_{z, o}$	unpolarised, natural light

Natural light is not monochromatic but of a broad spectral range, $φ$ changes statistically permanent. The y and z components are not coherent to each other.

Partially polarised light is made of polarised and unpolarised light. It is characterised through the degree of polarisation:

p = (Intensity of the polarised part)/Total intensity

For the characterisation of partially polarised light, four quantities are needed: The values of