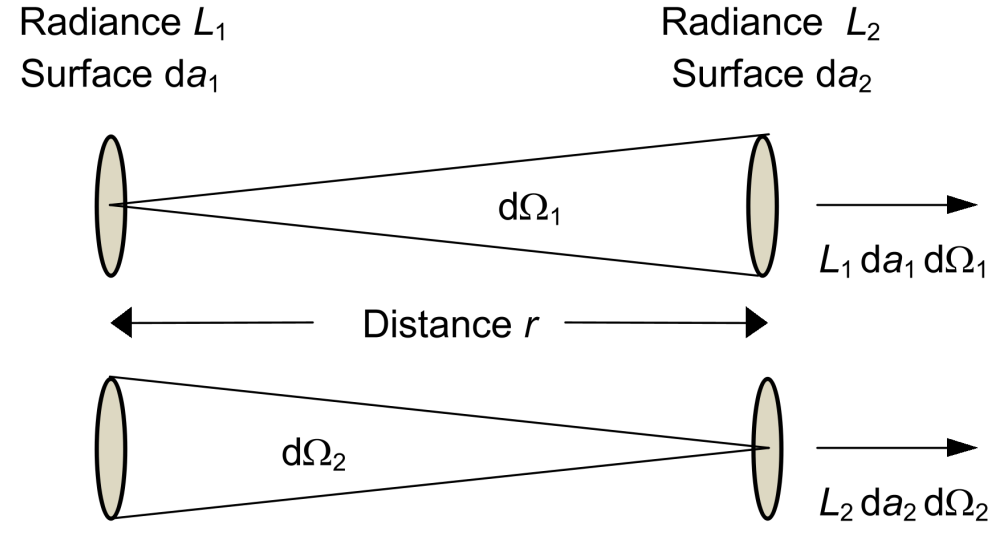Supplément 1.7: Grandeurs radiatives et radiométrie      (6/9)

La radiance (en englais : radiance)
aussi : la luminance énergétique, la densité de rayonnement

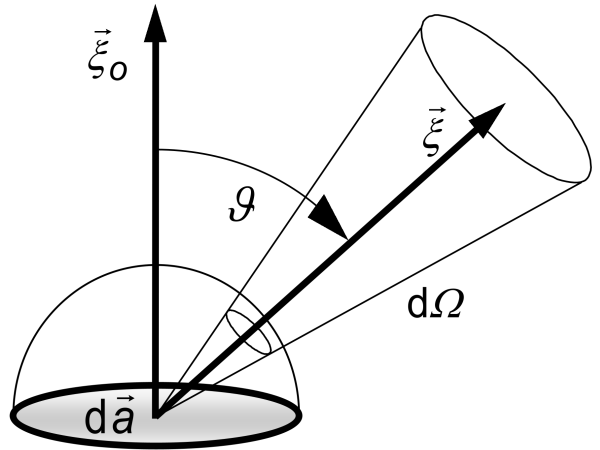
La radiance L est la grandeur radiométrique la plus fondamentale. Elle regroupe toutes les dépendances mentionnées jusqu'à présent : le flux énergétique ϕ, la surface rayonnante (ou irradiée) a, une direction dans l'espace et l'angle solide Ω autour de cette direction.

La radiance caractérise le flux énergétique émis par la surface dans cet angle solide :

Symbole: $L$
Unité de mesure: watt par stéradian par mètre carré, $\left[L\right]=\frac{\text{W}}{{\text{m}}^2\cdot \text{sr}}$

La radiance d'une surface da dans un angle solide dΩ autour de la direction $\overrightarrow{\xi }$. La surface da vue depuis cette direction apparaît réduite de cosϑ. ${\overrightarrow{\xi }}_o$ est le vecteur normal sur da.

La particularité de la radiance : il s'agit d'une propriété caractéristique de la source de rayonnement. Sa valeur reste inchangée lors de la propagation du rayonnement dans l'espace, dans la mesure où aucune modification n'intervient par absorption ou diffusion. À mesure que la distance par rapport à la source augmente, l'angle solide Ω englobe d'une part une surface qui augmente de manière quadratique. D'autre part, cela est compensé par la diminution quadratique de l'intensité du rayonnement sur la surface, ce qui explique pourquoi la radiance reste inchangée. Le graphique suivant illustre clairement ce phénomène.

Deux surfaces opposées da₁ et da₂. La surface gauche émet avec une radiance L₁, la surface droite reçoit la radiance L₂.

En haut, la situation est représentée du point de vue de la surface rayonnante da₁, en bas, du point de vue de la surface irradiée da₂. Il est évident que :

En utilisant les relations données dans le graphique, on obtient $L_1=L_2$.