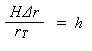Relief Displacement: Calculating Height

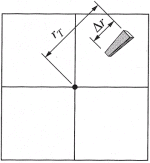
The magnitude of the displacement in the image between the top and the bottom of an object is its relief displacement and is related to:

  • the height of the object
  • the distance from the nadir point
What is the image nadir point ? ↓

We can derive an expression for the relationship between object height and relief displacement using the geometry depicted in following picture.

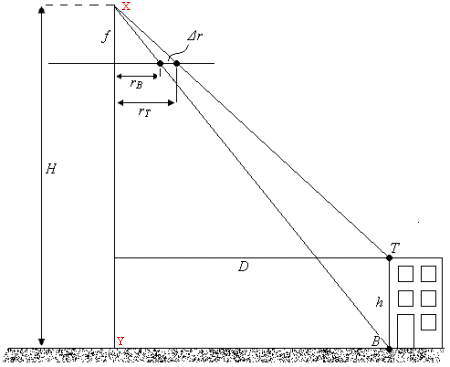
X is the perspective center, Y is the image nadir point

We may write two expressions for distance D in this figure, in terms of radial image distances rB and rT.

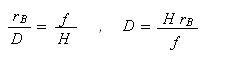
and

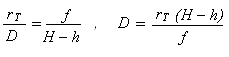
and set the two expressions for D equal to each other,

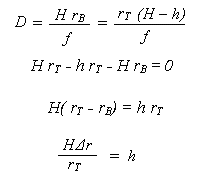
The last equation tells us that the flying height above the base of the object (H) times the relief displacement in the photograph (Δr) divided by the radial distance from the principal point to the top of the object (rT) is equal to the height of the object (h).

If all object units are the same (e.g., meters) and all image units are the same (e.g., millimeters), the units of the equation will be consistent.

Hence, if we know the flying height, we can calculate the height of any object in a photograph!

The height of an object can be estimated from a single aerian photograph provided we have one auxiliary piece of information, the flying height.

Example

The flying height above the base of the building shown in the following figure is 500 m for a vertical photograph H. When measuring the image, the relief displacement of the building (Δr) is 4 mm and the radial distance from the principal point to the top of the object (rT) is 75 mm.

What is the height of the building?

Solution ↓