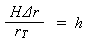Déplacement dû au relief : Calcul de la hauteur
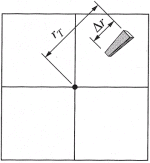
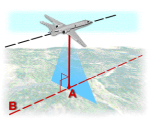
La distance mesurée dans l'image entre le sommet et la base d'un objet s'appelle le déplacement dû au relief et est fonction de :
- La hauteur de l'objet
- La distance au point nadir
On peut exprimer la relation entre la hauteur de l'objet et le déplacement dû au relief en utilisant la géométrie, comme illustré dans le schéma suivant.
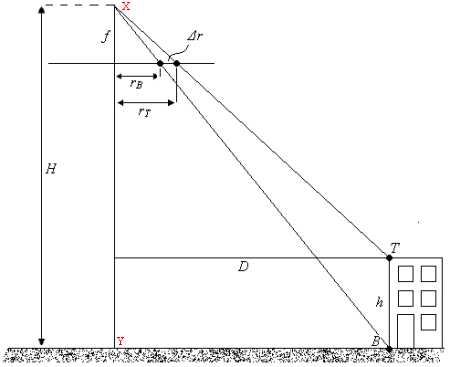
Nous pouvons exprimer la distance D par rapport à la distance radiale mesurée dans l'image de deux manières : rB et rT.
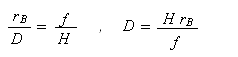
et
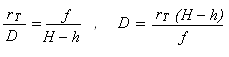
en égalant les deux expressions de D on a
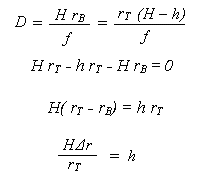
La dernière équation indique que la hauteur de vol au-dessus de la base de l'objet (H) multipliée par le déplacement dû au relief mesuré dans la photo (Δr), divisée par la distance radiale du point principal au sommet de l'objet (rT) est égale à la hauteur de cet objet (h).
Si toutes les unités relatives à l'objet sont identiques (par exemple, en mètres) et si toutes les unités-image le sont aussi (par exemple millimètres), les unités de l'équation en découleront logiquement.
Dès lors, si l'on connait l'altitude de vol, il est possible de calculer la hauteur de n'importe quel objet de la photo !
Exemple
La hauteur de vol H par rapport à la base du bâtiment représenté dans le dessin suivant est de 500 m pour une photographie verticale. Quand on mesure le déplacement dû au relief dans l'image (Δr), on obtient 4 mm et la distance radiale entre le point principal et le somment du bâtiment (rT) vaut 75 mm.
Quelle est la hauteur du bâtiment ?