2. Einführung in die mathematischen Methoden

Kovarianz und Korrelation (1/2)

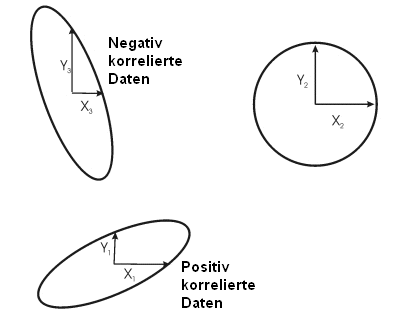
Wir haben gesehen, dass Daten korreliert sein können, d.h. beim Anstieg eines Parameters nimmt auch ein zweiter Parameter zu. In diesem Fall weisen die Streudiagramme die Struktur einer Linie auf, die in dem Diagramm diagonal von unten links nach oben rechts verläuft. Wie kann man solche Korrelationen messen und wie lassen sie sich veranschaulichen?

Um dies zu tun, wird die Varianzgleichung aus dem Kapitel Streuungsmaße abgeändert und als Kovarianz bezeichnet. Aus der Kovarianz wird die Korrelation abgeleitet.

Die Varianzgleichung war:

Ähnlich lässt sich die Kovarianz zwischen den Variablen x und y einer Stichprobe folgendermaßen berechnen:

Nun können wir eine Matrix aus den Werten der Varianz und der Kovarianz bilden:

In dieser Matrix sind nur zwei Variable (x und y) enthalten, daher entsteht ein (2,2)-Datenfeld. Das kann man für jede Variablenzahl machen; für n Variablen würde man also eine (n,n)-Matrix der Kovarianz erhalten. In einer Kovarianz-Matrix stellen die diagonalen Elemente von oben links bis unten rechts die Varianzen dar. Die Werte, die nicht auf dieser Diagonalen liegen, sind die Werte der Kovarianz.

Die Korrelation zwischen x und y ist dann:

Die Korrelationsmatrix wird also gebildet, indem die Werte in jeder Zeile durch die Standardabweichung in dieser Zeile und die Werte in jeder Spalte durch die Standardabweichung in dieser Spalte geteilt werden. Für zwei Variablen erhalten wir